Bootstraps et intervalles de confiance

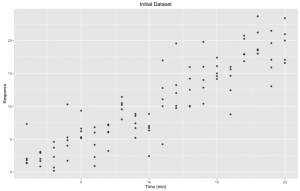
Figure 1. Ensemble de données initial: Réponse à travers le temps (minutes). Pour chaque point de temps, il y a cinq (5) réplicats.

Ayant ce jeu de données ainsi que des connaissances antérieures sur la tendance que nous devrions observer, nous aimerions ajuster un modèle non-linéaire à ces points. Plus précisément, nous voulons ajuster $ y = ax^{2} + b $. L’ajustement même peut facilement être fait en utilisant la fonction R nls. Présentement, nous utilisons l’approche des moindres carrés. Ayant une fonction à ajuster to.fit et un ensemble de données observées (x, y ),  nls estimera des valeurs pour nos deux paramètres a et b.

fit <- nls(y ~ to.fit(x, a, b), start = list(a = 1.0, b = 1.0))

Le résultat est présenté sous forme de tableau à partir duquel nous pouvons facilement récupérer les estimations ainsi que d’autres statistiques utiles. Nous avons maintenant notre  yfit, c’est-à-dire notre courbe ajustée!

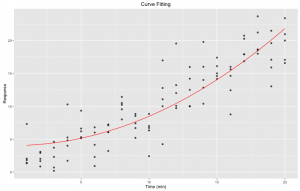
Figure 2. Courbe ajustée: ajustement non-linéaire des moindres carrés d’une équation pré-définie sur notre ensemble de données initial en utilisant la fonction nls de R. Nous avons utilisé predict(fit) pour générer les yfit. La courbe ajustée est représentée en rouge.

Ça, c’est un beau graphique! Cependant, comment pouvons-nous évaluer la qualité de notre ajustement? Comment savons-nous que nos données suivent en effet la tendance attendue? Plutôt que d’utiliser uniquement nos yeux et notre intuition, nous allons bootstraper! En d’autres mots, nous allons répéter notre ajustement m fois en utilisant n points de données provenant de notre ensemble initial et dériver un intervalle de confiance à partirc de toutes ces nouvelles courbes. Pour ce faire, nous utiliserons deux librairies R: broom et dplyr. Il se peut que vous aillez à installer les paquets avant de pouvoir importer les librairies mêmes (oublier cette étapes pourrait mener à des messages d’erreur et à beaucoup de frustration). broom a une fonction bootstrap automatisée qui peut vous sauver beaucoup de temps.

boot <- 1000
set.seed(2000)
df <- data.frame("x" = x, "y" = y)

Nous devons d’abord définir le nombre de fois que nous voulons répéter notre ajustement. Un plus grand boot nécessite généralement plus de temps à rouler, mais pourrait également se traduire en un intervalle de confiance plus précis. Ici, nous travaillerons avec  1000 bootstraps.

bt <- df %>% bootstrap(boot) %>%
 do(tidy(nls(y ~ to.fit(x, a, b), ., start = list(a = 1.0, b = 1.0))))

Dans cette étape, nous demandons de faire $m = boot$ ajustements de courbes. Chaque ajustement se fera sur un « nouvel » ensemble de données qui sera construit en choisissant au hasard $n$ points de notre jeu de données initial, où $n$ est le nombre de données dans l’ensemble initial. Les répétitions sont permises dans cette sélection aléatoire. Une fois ce « nouveau » jeu de données fait, nous appliquons la même approche d’ajustement qu’avant. Au final, nous aurons $m$ estimations pour chacun de nos paramètres.

bt.all <- df %>% bootstrap(boot) %>%
 do(augment(nls(y ~ to.fit(x, a, b), ., start = list(a = 1.0, b = 1.0)), .))

Comparé à l’extrait présenté où nous n’avions que les estimations de paramètres, nous générons maintenant les valeurs yfit de tous les échantillons bootstrap. Avec ces valeurs et les x qui leur correspondent, nous sommes en mesure de tracer les différentes courbes bootstrap. Notez qu’ici les x sont spécifiques à chaque bootstrap et ne correspondent donc pas nécessairement à nos x initiaux.

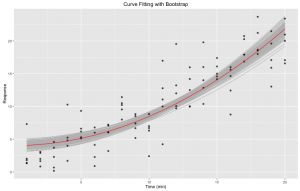
Figure 3. Courbe ajustée avec bootstrap: ajustement non-linéaire des moindres carrés d’une équation pré-définie sur notre ensemble de données initial en utilisant la fonction nls de R. 1000 bootstraps ont été générés en utilisant la fonction bootstrap de la librairie R broom. La courbe ajustée est représentée en rouge. Les courbes bootstrap sont représentées en gris.

La zone grise définie par les différents bootstraps peut être utile lorsque nous évaluons la qualité de notre ajustement. Cela étant dit, ce n’est pas toujours suffisant: dans certains cas, nous pourrions avoir une ou plusieurs courbes aberrantes. Par exemple, un échantillon bootstrap pourrait être composé d’un même point $n$ fois, ce qui résulterait en une drôle de courbe ne correspondant pas aux autres. Nous ne voulons pas ce genre de courbes dans notre graphique, mais nous ne pouvons pas non plus les enlever manuellement. Premièrement, la tâche ne serait pas simple et deuxièmement, nous ne pouvons tout simplement pas manipuler nos données d’une telle manière. À la place, nous allons générer un intervalle de confiance !

Nous devons générer un tableau fitted dont les colonnes sont les valeurs x  de notre ensemble initial, et dont les rangées sont les yfit pour chaque bootstrap. Il faut faire attention ici: les yfit sont calculés en utilisant les x initiaux plutôt que les x correspondant à chaque bootstrap. Cela veut dire que nous ne pouvons pas utiliser les mêmes yfit que ceux tracés! Nous devons utiliser les estimations de paramètres et calculer chaque yfit en utilisant nos x initiaux.

alpha <- 0.05
lower <- (alpha / 2) * boot
upper <- boot - lower

Nous allons calculer un intervalle de confiance de 95%, avec bornes supérieure et inférieure. Encore une fois, un plus grand boot faciliterait la tâche. Disons que nous avons $boot = 100$. Lorsque nous calculons les bornes, nous obtenons $ lower = \frac{0.05}{2} 100 = 2.5$ et $upper = 100 – 2.5 = 97.5$. Pour des raisons d’intégrité de type, les deux valeurs devront être arrondies. Le résultat serait alors un intervalle de confiance qui n’est pas tout à fait de 95%. En utilisant $boot ≥ 1000$ nous n’avons plus ce problème.

ci.sorted <- apply(fitted, 2, sort, decreasing = F)

Nous trions maintenant individuellement les colonnes de notre table en ordre croissant. Par conséquent, pour tout x, nous avons le maximum et le minimum des valeurs générées par bootstrap.

ci.upper <- ci.sorted[upper,]
ci.lower <- ci.sorted[lower,]

Et maintenant, nous construisons l’intervalle. Notre borne inférieure est définie par les valeurs de la rangée correspondant à notre lower calculé. Puisque que chaque colonne est triée en ordre croissant, cette rangée représente les valeurs au seuil $\frac{\alpha}{2}$. Inversement, la rangée upper représente le seuil $1 – \frac{\alpha}{2}$.

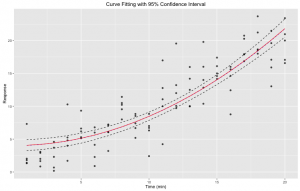
Figure 4. Courbe ajustée avec intervalle de confiance de 95%: ajustement non-linéaire des moindres carrés d’une équation pré-définie sur notre ensemble de données initial en utilisant la fonction nls de R. 1000 bootstraps ont été générés en utilisant la fonction bootstrap de la librairie R broom. L’intervalle de confiance fut calculé à partir des données de bootstrap. La courbe ajustée est représentée en rouge. Les courbes de l’intervalle sont représentées en pointillé.

Alors voilà! Nous avons maintenant une meilleure idée de la qualité de notre ajustement!