L’étude de la réponse cellulaire face à un composé chimique est cruciale au développement de nouvelles molécules thérapeutiques. Une telle analyse se fait généralement par expérience de criblage, où les cellules (spécifiques à une maladie, telle la leucémie) sont exposées aux composés chimiques d’intérêt pour différentes concentrations. La réponse ou la sensibilité de ces cellules est conventionnellement quantifiée par la valeur de l’IC50 ou de l’EC50. Voici quelques notions importantes à garder en tête lorsque nous analysons ces valeurs.
IC50/EC50 : estimation de la valeur relative
L’IC50 (de l’anglais inhibitory concentration) est la concentration pour laquelle la réponse est la moitié de celle du contrôle. Comme son nom l’indique, cette valeur est applicable lorsque la réponse analysée est l’effet inhibiteur de la molécule. Lorsque la réponse analysée correspond plutôt à l’activité de la molécule, au niveau de la croissance cellulaire par exemple, il est alors question d’EC50 (de l’anglais effective concentration). Cette valeur est donc la concentration pour laquelle la réponse est la moitié de la réponse maximale.
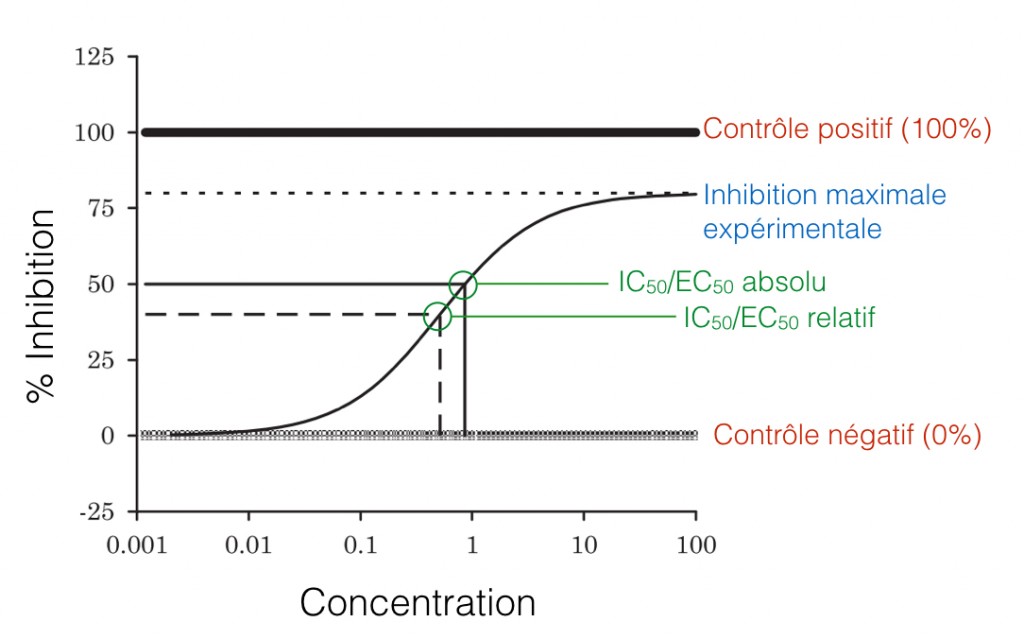
Figure 1. Réprésentation graphique des IC50/EC50 absolu et relatif. La courbe représente le % d’inhibition d’un composé chimique selon sa concentration: la réponse-50% correspond alors à l’EC50. Les contrôles positif et négatif servent à déterminer l’IC50/EC50 absolu, tandis que le contrôle négatif et l’inhibition maximale expérimentale servent à déterminer l’IC50/EC50 relatif. (Adapté de Sebaugh)
Lorsque le modèle log-logistique à 4 paramètres est utilisé pour estimer la réponse-50%, il faut garder en tête que la valeur du paramètre c est en fait l’IC50/EC50 relatif. Relatif puisque l’estimation correspond à la valeur à mi-chemin entre les réponses maximales et minimales: le paramètre c est alors grandement dépendant de l’estimation des paramètres a et d.
$$réponse = \frac {a-d} {1 + 10^{b \cdot {\left( \log_{10} c-{\log_{10} concentration}\right )}}} + d$$
Équation 1. Modèle log-logistique à quatre paramètres, définissant la réponse selon la concentration ($log_{10}$) de composé chimique. Les plateaux inférieur et supérieur sont définis par $a$ et $d$. L’IC50/EC50 relatif correspond à $c$, et la pente de la courbe par $b$. Chaque paramètre est optimisé par régression non-linéaire.
Pour travailler avec la valeur absolue, il faut utiliser une deuxième équation prenant pour paramètres les estimations obtenues précédemment. Une deuxième régression est alors nécessaire. Le protocole expérimental doit aussi être légèrement altérer, notamment par l’addition de contrôles pour une réponse maximale (contrôles positifs). Sebaugh décrit bien la démarche à suivre.
Donc, lorsque nous analysons la courbe dose-réponse pour un composé donnée, il est important de regarder l’IC50/EC50 dans un contexte plus large que sa simple valeur. Par exemple, l’absence d’un plateau supérieur évident pourrait indiquer un IC50/EC50 supérieur à sa “vraie” valeur. Sebaugh déclare qu’il faut un minimum de 2 concentrations sur chacun des plateaux pour assurer un IC50/EC50 relatif précis. La sélection du nombre et des valeurs des concentrations est alors cruciale.
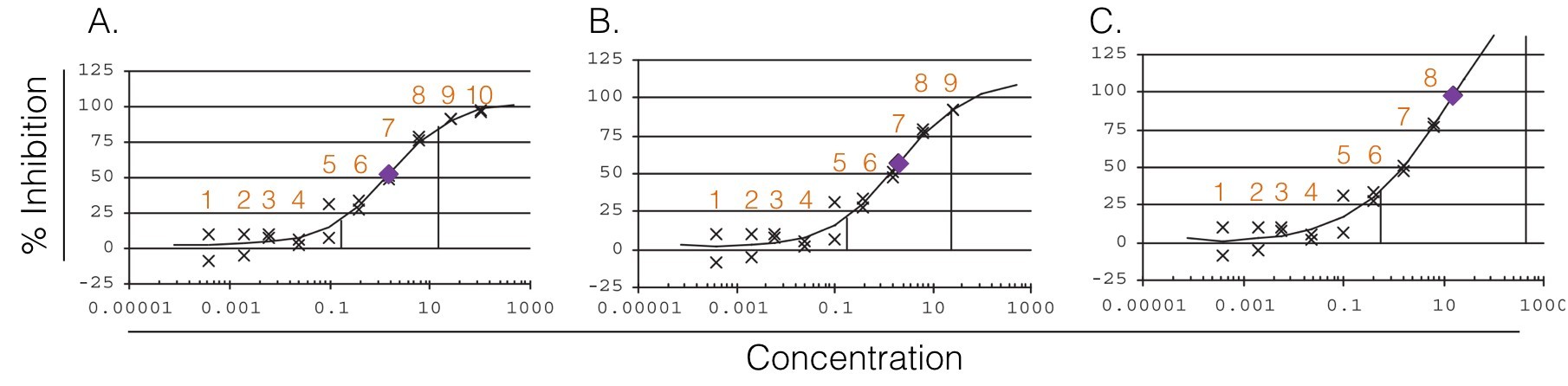
Figure 2. Représentation des effets du nombre de concentrations présent sur le plateau supérieur. Les plateaux sont définis par des points d’inflexion (lignes verticales) tel que décrit par Sebaugh et McCray. A. Le plateau inférieur comprend 5 concentrations, le supérieur 2 concentrations et l’IC50/EC50 relatif est estimé à 1.57. B. Le plateau inférieur comprend 5 concentrations, le supérieur 1 concentration et l’IC50/EC50 relatif est estimé à 2.04. C. Le plateau inférieur comprend 6 concentrations, le supérieur 0 concentration et l’IC50/EC50 relatif est estimé à 15.33.(Adapté de Sebaugh)
Extrêmes fixes ou ajustés?
D’un point de vue purement biologique, il est justifiable de vouloir fixer les valeurs des réponses minimale et maximale avant le processus d’optimisation: il est vrai qu’à concentration 0 le composé chimique ne devrait avoir aucun effet sur les cellules, et qu’à concentration infini il ne reste plus aucune cellule. Cela étant dit, dans le dernier cas, est-il correcte d’assumer que l’absence de cellules est réellement une cause de l’effet du composé chimique? Ce pourrait-il, qu’à concentration infinie il y ait d’autres facteurs affectant la survie des cellules (un manque de nutriments par exemple)?
Je trouve toujours intéressant de commencer mon analyse en ajustant un modèle log-logistique à 4 paramètres, c’est-à-dire en ne fixant pas les réponses maximale et minimale. L’estimation des extrêmes peut alors mettre en lumière certains aspects de l’analyse. Par exemple, un minimum négatif pourrait indiquer qu’il y ait une erreur avec le processus de normalisation des données par rapport aux contrôles négatifs ou qu’il y ait un problème à même les contrôles négatifs. Généralement, lorsque l’estimation du minimum est autours de 0, nous sommes sur une bonne voie. Maintenant, l’évaluation du maximum n’est pas toujours aussi évidente: un maximum expérimental n’atteignant pas 100% n’est pas nécessairement mauvais.
Cela étant dit, je continue mon analyse en ajustant une deuxième courbe avec des extrêmes fixes, et une troisième pour laquelle seule le minimum est constant. Comparer les valeurs des différents paramètres aide à acquérir une meilleure compréhension de ce que les “vraies” valeurs devraient être. Il est aussi intéressant de regarder les effets de ces paramètres fixes sur lesIC50/EC50.
Le plus important est, selon moi, de trouver un juste milieu entre ce qui biologiquement réaliste et ce qui est mathématiquement valable.
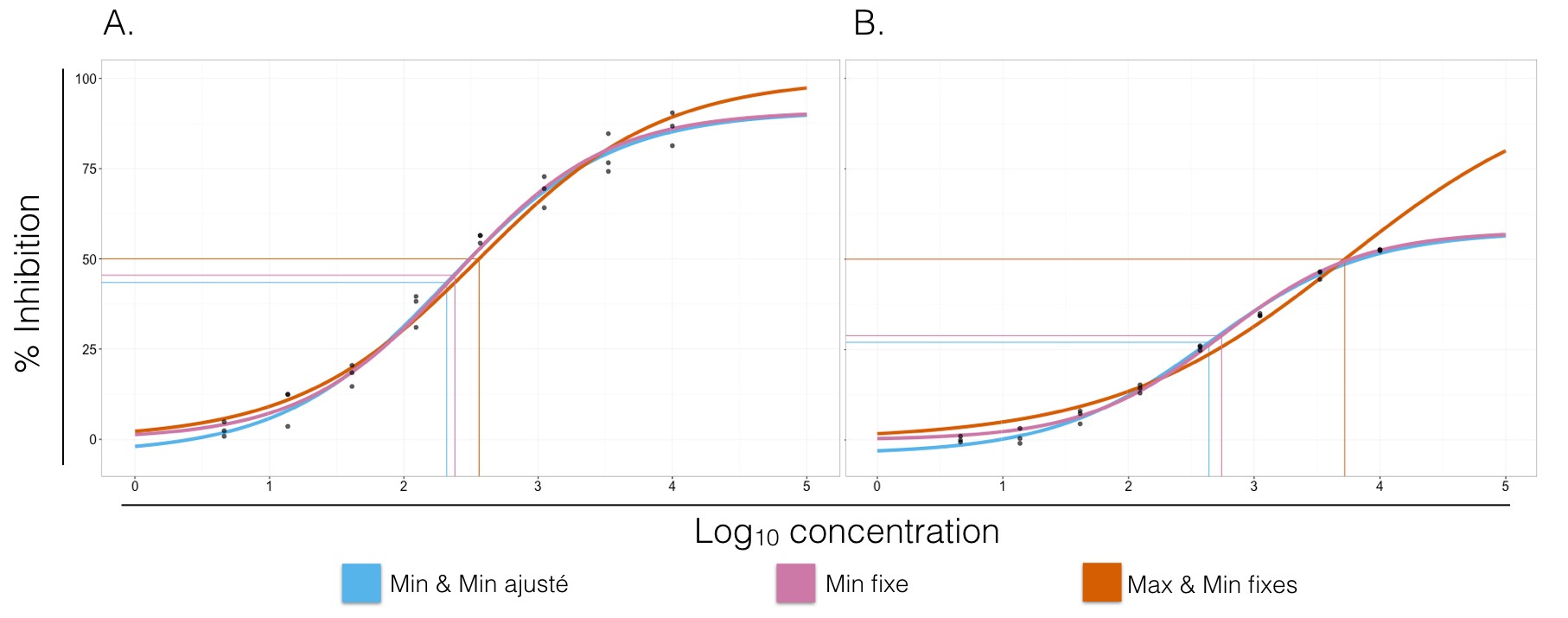
Figure 3. Courbes dose-réponse pour deux jeux de données différents (A et B). Les courbes bleues n’ont aucun paramètres constants lors de l’ajustement du modèle log-logistique. Les courbes roses possèdent une réponse minimale (paramètre $a$) constante à 0%. Les courbes oranges ont, quant à elles, une réponse minimale et maximale constantes à 0% et 100%, respectivement. Les IC50/EC50 de chaque courbe sont représentation par la jonction des droites horizontale et verticale de même couleur. A. Bleue: $a = -4.07$, $d = 91.02$, $c = 2.30$ et $b = -0.75$. Rose: $a = 0.00$, $d = 90.90$, $c = 2.37$ et $b = -0.78$. Orange: $a = 0.00$, $d = 100.00$, $c = 2.47$ et $b = -0.65$. Les paramètres sont sensiblement les mêmes. B. Bleue: $a = -3.27$, $d = 58.08$, $c = 2.70$ et $b = -0.71$. Rose: $a = 0.00$, $d = 57.79$, $c = 2.75$ et $b = -0.81$. Orange: $a = 0.00$, $d = 100.00$, $c = 3.75$ et $b = -0.48$. Les paramètres estimés lorsque $a$ et $d$ sont fixes divergent grandement de ceux des deux autres courbes.
Les décisions prises par rapport à l’évaluation de l’efficacité d’un composé chimique sont grandement relié au protocole expérimental utilisé lors du criblage. Par exemple, l’ajout de contrôles positifs permet le calcul de l’IC50/EC50 absolu plutôt que relatif. Il est important de toujours réviser sa méthode d’analyse de l’efficacité, de telle sorte que les conclusions tirées est un fondement solide. Il est aussi intéressant de remarquer que plusieurs publications traitent de nouvelles approches spécifique à certains cas. Notamment, Hafner et al. proposent de nouvelles métriques tenant compte de la croissance cellulaire lors d’expérimentations avec de longues périodes d’incubation. Finalement, il est pratique d’avoir une idée de la méthode d’analyse d’efficacité avant de commencer l’expérience, puisque certaines nécessitent de légères modifications au protocole expérimental.


Laisser un commentaire