Un collègue m’a récemment demandé de produire une visualisation montrant l’expression différentielle des gènes entre deux échantillons (sans réplicats). En utilisant les données de RPKM, il voulait faire ressortir tous les gènes se trouvant aux extrémités de la distribution i.e. à 2 écart-types de la moyenne ou plus.
Comme premier essai, j’ai calculé la distribution de fold change et l’écart-type et j’ai tracé les droites correspondantes de chaque côté de la diagonale sur un graphe en nuage de points présentant les deux échantillons :
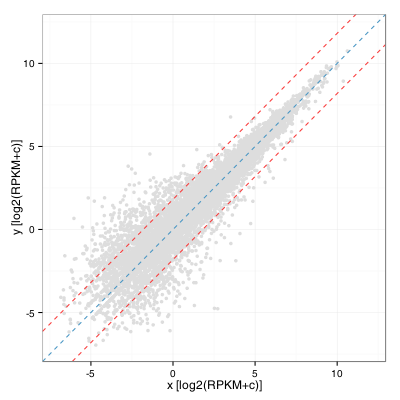
Ceci équivaut à calculer l’écart-type des valeurs résiduelles d’un modèle linéaire appliqué à cette distribution. En R :
sd(residuals(lm(y ~ x + 0)) ~= sd (log(FC))
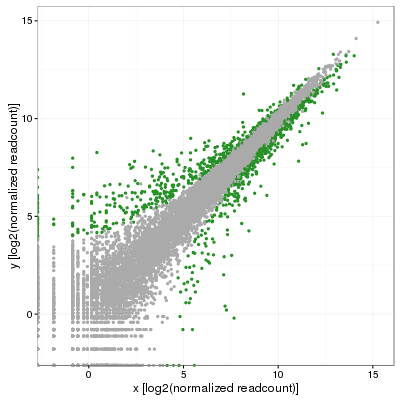
Mon collègue m’a vite fait remarqué que ce n’était pas tout à fait satisfaisant puisqu’il s’attendait à voir l’écart-type varier le long de la diagonale. Même si cela semblait logique, après plusieurs minutes de recherche, je ne voyais pas comment arriver à le satisfaire. Éventuellement, nous avons obtenu des réplicats pour ce projet et j’ai pu faire une analyse complète de l’expression différentielle en utilisant le logiciel DESeq2. J’ai pu utiliser les p-values ajustées pour colorer les gènes significatifs (p-adj < 0.001):
Projetons-nous plusieurs semaines plus tard. Sortant de nulle part, la réponse au problème original m’est apparue sous la forme d’un simple problème de géometrie. J’ai testé la solution suivante. D’abord, appliquer un modèle linéaire sur la distribution pour obtenir la pente (m) de la droite dérivée du modèle, qui devrait théoriquement être proche de 1 si les données sont normalisées correctement. Dans mon cas, j’ai obtenu une valeur de 0.986, ce qui n’est pas mauvais du tout. Ensuite, j’ai fait une rotation de la distribution en utilisant une valeur d’angle correspondant à la pente, ou atan(m), mais dans le sens des aiguilles d’une montre, donc Theta=-atan(m). On peut facilement convertir les coordonnées (x,y) en utilisant une matrice de rotation :
![]()
Nous pouvons ensuite calculer un écart-type par fenêtre sur les valeurs de y’ le long de l’axe des x’ et transformer ces valeurs en deux courbes en utilisant une rotation -Theta. Ceci donne :
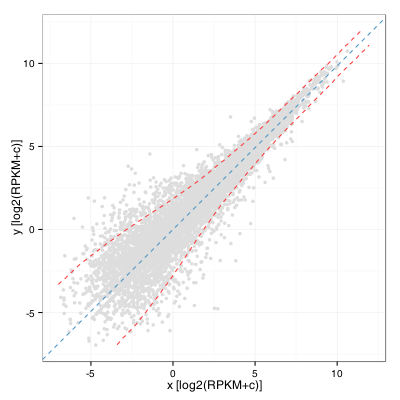
Un observateur avisé remarquera que cela revient presque à calculer l’écart-type par fenêtre sur les valeurs A le long de l’axe M sur un graphe MA. Ce serait en fait exactement la même chose si l’angle de rotation était de pi/4. Aussi, on remarquera que pour identifier les gènes intéressants, un seuil appliqué à l’écart-type n’est probablement pas la meilleure solution puisqu’on se retrouve à conserver beaucoup de gènes peu exprimés. Un seuil sur le niveau d’expression et sur le fold change reste la meilleure option lorsqu’on travaille sans réplicats.


Laisser un commentaire