L’objectif premier du scientifique des données (data scientist) est l’exploration de données afin d’en découvrir des relations d’intérêt. Des méthodes statistiques et d’apprentissage machine lui servent d’outils pour la découverte et la modélisation de telles relations. L’information découverte par ces méthodes peut ensuite être mise en pratique. Par exemple, en médecine clinique, l’élaboration d’un modèle prédictif basé sur des données cliniques peut servir d’outil prognostic afin de guider un traitement.
Régression linéaire simple
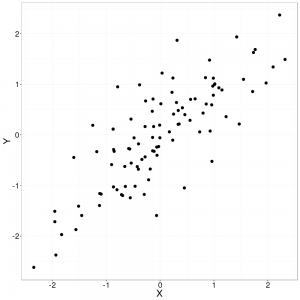
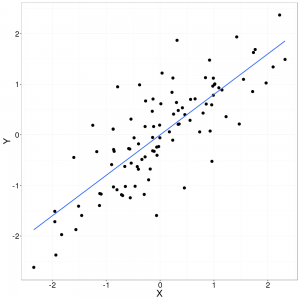
L’une des méthodes la plus simple à la disposition du scientifique des données est la régression linéaire où le cas le plus simple est une régression linéaire avec une seule variable explicative. C’est la régression linéaire simple. Opérant sur un ensemble d’observations de deux dimensions (deux variables continues), la régression linéaire simple tente tout simplement d’ajuster, le mieux possible, une droite parmi les données. Ici, « le mieux possible » signifie minimiser la somme des erreurs carrées, c’est-à-dire la distance entre un point et la droite (voir la méthode des moindres carrées). Pourquoi? Cette droite (notre modèle) devient alors un outil permettant de ressortir, si elle existe, la tendance sous-jacente dans les données en plus de servir comme modèle prédictif pour de nouveaux événements en se basant sur ceux déjà observés.
Bien qu’il soit tentant de suivre cette droite pour prédire des évènements à l’extérieur de nos observations, il faut faire attention à de telles prédictions puisque le modèle n’a pas été bâti en prenant compte de cet espace. Aucune information n’est disponible pour supporter cette extrapolation.
Tâche
Plus formellement, il s’agit de trouver la pente $m$ et l’ordonnée à l’origine $b$ pour une droite qui minimise la somme des erreurs (distances) carrées entre nos observations et la droite. Rappelons nous l’équation d’une droite :
$ y = m x + b$
Bien que la différence perpendiculaire représente une différence (ou erreur) plus exacte, seule la différence verticale (différence entre la valeur $y$ d’une observation et la valeur $y$ sur la droite de régression pour la même valeur $x$) est utilisée, simplifiant ainsi le calcul.
Approche naïve
Avertissement! Cette section et le code qui y est contenu est offert simplement comme exemple jouet. Sautez à la section « Approche analytique » pour la véritable solution!
Connaissant l’équation de la droite, serait-il réaliste de générer une multitude de droites avec pentes et ordonnées à l’origine aléatoirement choisies? Un simple calcul de l’erreur pour chaque droite nous indiquerait donc si elle représente une droite de régression approximant bien nos données. Malheureusement, cette tâche est bien trop ambitieuse. L’espace de recherche est infiniment grand! Une infinité de droites doivent être testées pour aboutir à la solution optimale. Même si l’on se contente d’une solution non optimale, cette technique peut réalistement seulement fonctionner si la recherche est sévèrement bornée. Voici un brin de code python implémentant cette idée loufoque.
import random
def error(m, b, X, Y):
assert(len(X) == len(Y))
return sum(((m*x+b) - Y[idx])**2 for idx, x in enumerate(X))
def naive_LR(X, Y, n):
assert(len(X) == len(Y))
best_error = None
best_m = None
best_b = None
for i in range(0,n):
# Attention! valeurs des bornes de m et b doivent êtres
# ajustées en fonction des données!
m = random.uniform(-100, 100)
b = random.uniform(-100, 100)
error = error(m, b, X, Y)
if error < best_error:
best_error = error
best_m = m
best_b = b
return best_error, best_m, bSurprenament, lors de mes tests, cette implémentation semblait quand même trouver une droite assez bien ajusté. Le succès de ce code dépend largement de la sélection de bornes pour les valeurs possibles de $m$ et $b$. Ici, les bornes ont été sélectionnées plus ou moins aléatoirement en étant sûr de sélectionner des valeurs beaucoup plus grandes que les extrêmes retrouvés dans notre jeu de données. Bien sûr, de meilleurs heuristiques peuvent êtres concoctées pour la sélection de telles bornes (avec comme conséquence de rendre notre solution moins naïve). Finalement, le nombre de droites à générer, $n$, doit lui aussi être fixé. Le nombre de droites générées augmente le nombre chances de trouver une droite bien ajustée tout en augmentant le temps de calcul.
Approche analytique
Heureusement, ce type de problème est assez simple pour qu’une solution purement analytique existe. Comme nous l’avons décrit plus haut, c’est la sommation de la distance verticale entre nos observations et la droite de régression au carrée qui nous sert de fonction de coût et cela est ce que nous tenons à minimiser. Elle se résume ainsi :
$ cost = \sum_{i=1}^n(y_i-\hat{y_i})^2 $
En y insérant l’équation de la droite :
$ cost = \sum_{i=1}^n(y_i-(m x_i + b))^2 $
De cette fonction, on y isole la pente. Notez qu’une barre placée sur une variable (ex. $\bar{x}$) représente la moyenne de cette variable dans nos observations.
$ \hat{m} = \frac{ \sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y}) }{ \sum_{i=1}^n (x_i – \bar{x})^2 } $
Une fois trouvée, cette valeur peut être introduite dans l’équation de la droite pour y trouver l’ordonnée à l’origine $b$.
$ \hat{b} = \bar{y}-\hat{m}\,\bar{x} $
(Une manipulation mathématique plus détaillée peut être retrouvée dans l’article wikipédia anglais de la régression linéaire simple et dans les notes d’un cours de stats de l’université de la Floride.)
Le code :
def mean(l):
return float(sum(l)) / len(l)
def analytical_LR(X, Y):
assert(len(X) == len(Y))
mean_x = mean(X)
mean_y = mean(Y)
num = sum((X[idx] - mean_x)*(Y[idx] - mean_y) for idx in range(len(X)))
denum = sum((X[idx] - mean_x)**2 for idx in range(len(X)))
m = num / float(denum)
b = mean_y - m*mean_x
error = error(m, b, X, Y)
return error, m, b
Approche itérative – descente de gradient
Une solution peut aussi être trouvée par descente de gradient. Cette méthode tente d’approcher une solution optimale en ajustant petit à petit les paramètres de la fonction à optimiser. Bien qu’il soit possible de trouver une solution à une régression linéaire simple avec cette méthode, elle est généralement utilisée dans le cadre de régression non linéaire où une solution analytique requerrait un calcul prohibitif ou est simplement non disponible. La descente de gradient est une méthode grandement utilisée en apprentissage machine lors de, entre autres, l’entrainement de réseaux de neurones. Elle permet d’obtenir rapidement une solution approximative à un problème complexe.
Cette approche sera couvert dans un prochain article. Restez à l’écoute!


Laisser un commentaire