Lorsqu’on travaille avec des données liées au cancer, un de nos objectifs est parfois de trouver des caractéristiques (mutation, information clinique, expression génique, …) associées au prognostic, i.e. des caractéristiques reliées à l’évolution probable de la maladie.
Si c’est aussi l’un de vos objectifs, vous aurez à faire une analyse de survie. Les analyses de survie sont constituées d’un ensemble de méthodes qui essaient de modéliser à quel moment un événement d’intérêt apparaîtra (temps d’apparition), cet événement étant souvent le décès. En réalité, n’importe quel événement ayant un temps d’apparition intéressant pourrait être étudié (le temps avant l’apparition d’une infection après une chirurgie, le temps de rejet d’une greffe, le temps de récidive après une cure de désintoxication ou le temps avant qu’un premier ministre ne quitte le pouvoir — pas grand chose à voir avec la survie, je sais!–).
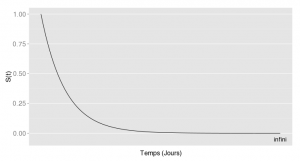
Dans une analyse de survie, vous essayez d’estimer la fonction de survie S(t), i.e. la probabilité que l’événement ne soit pas encore survenu au temps t. En théorie, la fonction S(t) ressemblerait à ceci :
Au tout début, personne n’a encore vu l’événement. Et si on avait infini de temps (donc dans vraiment longtemps!!), l’événement arriverait à tout le monde (particulièrement si l’événement est le décès). Je suis certaine que vous avez déjà vu des courbes de survie, mais qu’elles ne ressemblaient pas tout à fait à cela.
En pratique, un des problèmes majeurs rencontrés est que vous ne connaissez pas tous les temps de survie de tous les individus étudiés. Pour la plupart, vous saurez que l’événement est survenu au temps t, mais pour d’autres, vous n’aurez pas cette information. Vous saurez seulement que l’événement n’est pas survenu au moment où les données ont été collectées. La personne peut être sortie de l’étude. Elle peut avoir été perdue de vue. L’étude peut s’être terminée avant que l’événement ne survienne. On appelle cela « censure ».
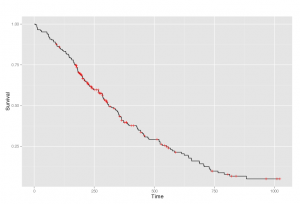
L’estimateur produit-limite de Kaplan-Meier est utilisé en pratique pour gérer les données censurées et estimer la fonction de survie. Les courbes que vous avez vues étaient sûrement des graphes de Kaplan-Meier. avec chacune des censures indiquée par un petit trait vertical.
Regardons de plus près comment construire ces courbes!
Normalement, vous débuterez votre analyse avec des données dans le format suivant:
| Id.Échantillon | Survie (jours) | Censure (décédé=1; vivant=0) |
| TCGA-05-4395-01 | 0 | 1 |
| TCGA-56-7822-01 | 1 | 0 |
| TCGA-85-7699-01 | 1 | 0 |
| TCGA-56-A4BW-01 | 2 | 0 |
| TCGA-85-8664-01 | 3 | 0 |
| TCGA-56-5897-01 | 3 | 0 |
| TCGA-71-8520-01 | 3 | 0 |
| TCGA-56-A5DR-01 | 4 | 0 |
| TCGA-56-A4ZK-01 | 4 | 0 |
| TCGA-77-7338-01 | 5 | 1 |
| TCGA-94-7557-01 | 5 | 1 |
La prochaine étape est de transformer ce format en « life-table » (cette conversion peut être faite dans Excel en utilisant les formules matricielles).
| Jours | Nb. décès | Nb. censures |
| – | – | – |
| 0 | 1 | 0 |
| 1 | 0 | 2 |
| 2 | 0 | 1 |
| 3 | 0 | 3 |
| 4 | 0 | 2 |
| 5 | 2 | 0 |
Ensuite, vous devez calculer les probabilités :
| Jours | Nb. décès | Nb. censures | Nb de sujets | Probabilité de survie cumulative |
| – | – | – | – | 1 |
| 0 | 1 | 0 | 11 | 10/11 * 1 = 0.909 |
| 1 | 0 | 2 | 10 | 10/10 * 0.909 = 0.909 |
| 2 | 0 | 1 | 8 | 8/8 * 0.909 = 0.909 |
| 3 | 0 | 3 | 7 | 7/7 * 0.909 = 0.909 |
| 4 | 0 | 2 | 4 | 4/4 * 0.909 = 0.909 |
| 5 | 2 | 0 | 2 | 0/2 * 0.909 = 0 |
Pour chaque point dans le temps, on calcule la probabilité de survie en divisant le nombre de non événements par le total. On multiplie ensuite la probabilité du temps précédent (t-1) à la probabilité courante. Par exemple, au temps 0 (t=0), il y a 11 sujets au total dont un est décédé (l’événement est survenu). Il y a donc 10 (11-1) sujets qui n’ont pas vu l’événement. Ainsi, nous divisons 10/11 et nous multiplions par la probabilité précédente. Dans ce cas-ci, comme nous sommes au temps 0, nous assumons que la probabilité précédente est égale à 1.
Les analyses de survie sont faciles à effectuer en R et en Python (pour les fans de Python, j’ai déjà parlé du package lifelines ici). Vous trouverez d’ailleurs une liste de modules R liés à l’analyse de survie ici. En R, ce n’est pas plus compliqué que cela:
library(survival)
data(lung)
Y = Surv(lung$time, lung$status)
s = survfit(Y~1)
plot(s)Il y a aussi quelques outils disponibles en ligne (SurvCurv ou Oasis). Ils fonctionnent bien, mais nécessitent que les données soient soumises sous forme de « life-table« .


Laisser un commentaire