Permutations

Supposons que vous ayez ces deux groupes de données :

g1 <- c(55, 65, 58)
g2 <- c(12, 18, 32)

Nous voulons savoir si ces deux groupes appartiennent à la même distribution ou sont considérés comme deux groupes différents. Nous serions probablement tenté, pour élucider la question, d’appliquer un test de Student, le test-t.

t.test(g1, g2)

##  Welch Two Sample t-test
## 
## data:  g1 and g2
## t = 5.8366, df = 2.9412, p-value = 0.01059
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  17.34281 59.99052
## sample estimates:
## mean of x mean of y 
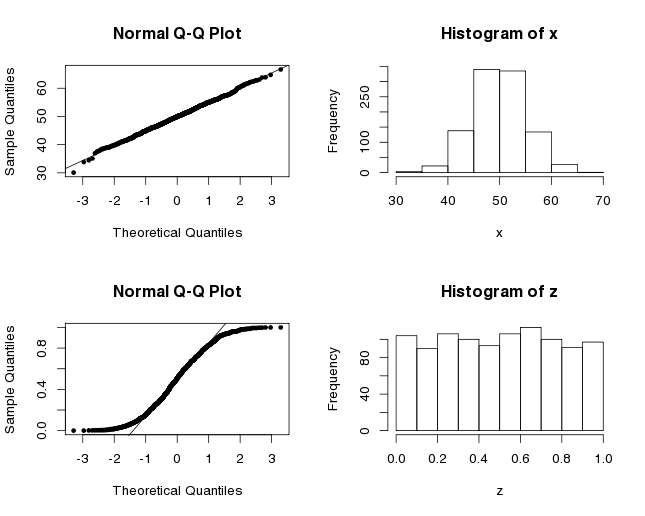
##  59.33333  20.66667

Le test t nous retourne un petit un p-value qui indique qu’il y a une différence significative entre les moyennes. Mais attendez, avons-nous le droit d’appliquer ce test statistique? Une des suppositions sous-jacentes au test de Student est que nos données suivent une distribution normale. Avec trois valeurs dans chaque groupe, il est difficile de déterminer si c’est le cas. D’habitude, le graphe Q-Q pourrait être utilisé pour déterminer si la distribution est normale. Cette méthode visuelle standard compare nos données aux quantiles théoriques de la distribution normale. Quand tous les points d’un ensemble de données s’alignent sur la droite, cela suppose que les données sont normalement distribuées. Ici, vous avez les graphes Q-Q pour x, qui est normalement distribué (puisque nous avons utilisé la fonction rnorm pour construire ce vecteur) et z qui est uniformément distribué.

x <- rnorm(1000, mean=50, sd=5) # distribution normale
z <- runif(1000) #distribution uniforme
par(mfrow=c(2,2))
qqnorm(x, pch=20)
qqline(x)
hist(x)
qqnorm(z, pch=20)
qqline(z)
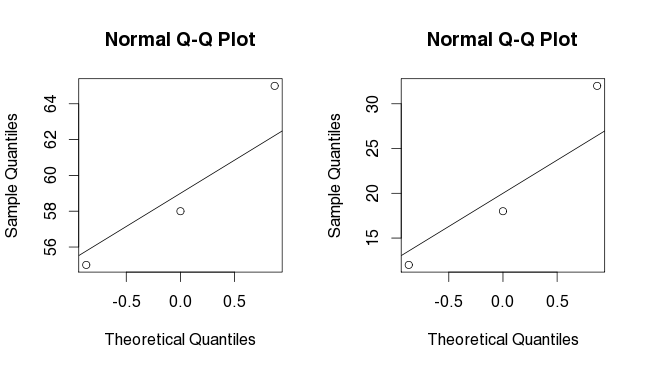
hist(z)

Si nous essayons la même chose pour nos deux vecteurs g1 et g2, nous n’obtenons pas beaucoup d’informations sur la distribution car nous n’avons pas assez de points.

par (mfrow=c(2,2))
qqnorm(g1)
qqline(g1)
qqnorm(g2)
qqline(g2)

Sans connaître la distribution de notre ensemble de données, nous pourrions décider de laisser tomber les tests paramétriques et d’utiliser un test non paramétrique. Le test U-Mann-Withney-Wilcoxon est un test non paramétrique largement utilisé. Il compare le rang des valeurs d’un ensemble de données et non les valeurs comme telles. J’ai déjà expliqué les premières étapes de ce test dans un (article précédent).

wilcox.test(g1, g2)

##  Wilcoxon rank sum test
## 
## data:  g1 and g2
## W = 9, p-value = 0.1
## alternative hypothesis: true location shift is not equal to 0

Le p-value obtenu avec wilcox.test est plus élevé que le p-value que nous avions calculé plus tôt.
Ici, vous devriez être conscient que le test t et le test u n’utilisent pas les mêmes hypothèses NULL et alternatives. Lorsque vous utilisez ces deux tests, vous ne testez pas tout à fait la même chose. Le test t vérifie si la vraie différence de moyennes entre les groupes est différente de zéro alors que le test u vérifie qu’une population particulière présente des valeurs plus élevées que l’autre, i.e. si les médianes sont égales. Nos données supportent ce constat. Pourquoi le test de u nous donne-t-il alors un p-value non significatif de 0.1? Parce que nous n’avons pas assez de valeurs à comparer!! Les valeurs de significance (dans la table de valeurs critiques de Mann-Withney U) ne sont même pas définies pour une comparaison 3 versus 3. C’est même surprenant que R nous retourne un p-value.

Et maintenant? Quoi faire? Ma première réponse est : obtenir plus de données!! Mais si c’est impossible, nous pouvons tenter d’appliquer un test de permutations. Quand l’ensemble de données est petit, le test de permutations complet peut être appliqué pour obtenir une distribution de permutations complète. Quand nous avons affaire à un plus gros ensemble de données (quand nous ne pouvons pas énumérer toutes les permutations), un test de permutations avec échantillonnage peut être utilisé. Dans ce cas, il est important de choisir les combinaisons aléatoirement et avec la même probabilité.

Comment ça fonctionne? D’abord, il faut calculer une statistique sur nos deux groupes à comparer : une différence de médianes, de moyennes, de sommes… Cette valeur deviendra la valeur observée, T(obs). Ensuite, nous devons mettre toutes nos données ensemble et brasser les étiquettes associées (groupe1/groupe2). Nous calculons la statistique pour toutes les permutations (ou pour
n répétitions). Lorsque nous avons terminé, nous pouvons compter le nombre de fois où la statistique « aléatoire » était meilleure que la statistique observée. Par définition, le p-value représente la probabilité qu’un test donne un résultat au moins aussi extrême que la valeur observée sous l’hypothèse null (ou plus simplement exprimé, la probabilité que la valeur observée ait été observée par chance). Ici, l’hypothèse null devient : les étiquettes sont assignées aléatoirement. Nous obtenons donc la probabilité d’observer notre statistique sous l’hypothèse que les étiquettes n’ont pas d’importance.

Tobs <- sum(g1)-sum(g2)
data <- c(g1, g2)
combinaisons <- t(combn(data,3, simplify=T))

diff <- function(data, combinaison_i=0, combinaisons=NULL) {
  # si nous n'énumérons pas toutes les combinaisons possibles, nous en choisissons au hasard
  if (combinaison_i==0) {
    x1 <- sample(data, 3, replace=F)
  }
  # nous énumérons toutes les combinaisons
  else {
    x1 <- combinaisons[combinaison_i,]
  }
  # La combinaison choisie a été attribuée au groupe1; les valeurs restantes forment le groupe2 
  x2 <- data[!data%in%x1]
  # Nous calculons et retournons notre statistique
  return (sum(x1)-sum(x2))
}

Trand <- c()
# Nous énumérons toutes les combinaisons retournées par la fonction combn()
for (i in 1:nrow(combinaisons)) {
  Trand <- c(Trand, diff(data, combinaison_i=i, combinaisons=combinaisons))
}
sum(Trand>=Tobs)/nrow(combinaisons)

## [1] 0.05

Pour un test avec échantillonnage, la fonction replicate est très utile car elle nous permet de répéter une expression plusieurs fois. Ici, nous avons choisi aléatoirement 3 valeurs pour faire partie du premier groupe et les valeurs restantes ont été mises dans le deuxième groupe. Nous répétons cela 1000 fois.

Puisqu’il y a 20 combinaisons pour le groupe 1 (choisir 3 parmi 6=20; n!/k!(n-k)! où n est le nombre total de choix et k est le nombre à choisir), nous sélectionnons les mêmes combinaisons plusieurs fois. En fait, une même combinaison est choisie en moyenne 50 fois.

# Nous ne listons pas toutes les combinaisons, nous choisissons une combinaison aléatoire et faisons cela n fois.
# Nous pouvons utiliser la même fonction que précédemment
n <- 1000
Trand <- replicate(n, diff(data=data))
sum(Trand>=Tobs)/n

## [1] 0.065

Le test de permutations complètes est probablement un meilleur choix ici.

Les tests de permutations (et les méthodes de ré-échantillonnage, bootstrapping) sont utiles dans plusieurs situations. Ici, j’ai illustré le problème des petits (minuscules?) ensemble de données, mais en réalité les tests de permutations ne sont pas limités à cette situation.

Je terminerai en disant que 3 échantillons, c’est souvent trop peu pour effectuer des tests statistiques! Planifiez votre travail en conséquence, car comme on dit : mieux vaut prévenir que guérir.