Mariana fut introduit précédemment sur ce blog en mai par Geneviève dans son article Apprentissage automatique en sciences de la vie.
Présentement à la version 1.0rc3 sur github, le lancement de la version 1.0 stable de Mariana approche maintenant à grands pas. Cette nouvelle version représente un remaniement de code important et ajoute plusieurs nouvelles fonctionnalités (une liste complète des changements incorporés dans la version 1.0 est disponible ici). Je profite de cette occasion pour présenter une petite capsule sur l’extension des fonctionnalités de Mariana 1.0.
Implémentation d’un réseau « Siamois »
La documentation de Mariana couvre un grand nombre de réseaux; tous déjà implémentés et facilement utilisables dans Mariana. Mais qu’en est-il des cas non couverts par Mariana? Si l’on veut utiliser Mariana mais que le réseau dont nous avons besoin n’est pas disponible?
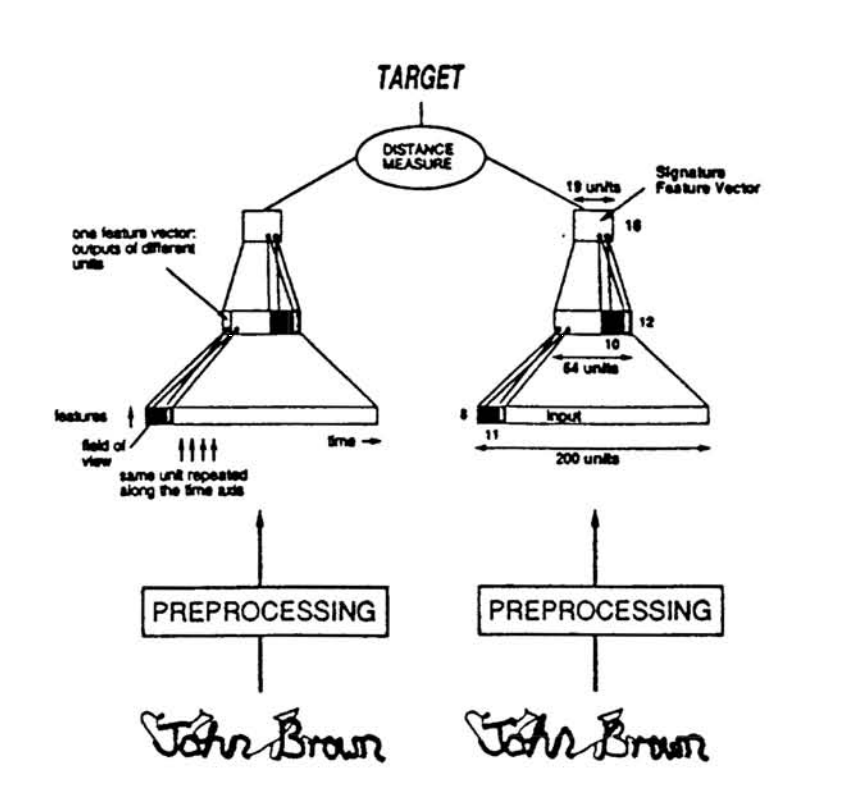
Heureusement, étendre la fonctionnalité de Mariana (i.e. ajouter des fonctions ou un nouveau type de réseau) se fait généralement sans trop d’efforts. Prenons comme exemple l’implémentation d’un réseau de type « Siamois » inspiré par le réseau décrit dans Signature Verification using a « Siamese » Time Delay Neural Network [1].
Dans cette exemple, le réseau « Siamois » essaie de détecter de fausses signatures. Il reçoit ainsi en entrée des paires de signatures véritables et de contrefaçons. Ce réseau « Siamois » est en fait composé de deux réseaux de type feed-forward dont les poids sont liés. La similarité cosinus des sorties des deux réseaux est utilisée comme mesure de distance.
$ \text{Similarité cosinus} = \cos(\theta) = {\mathbf{A} \cdot \mathbf{B} \over \|\mathbf{A}\| \|\mathbf{B}\|} = \frac{ \sum\limits_{i=1}^{n}{A_i B_i} }{ \sqrt{\sum\limits_{i=1}^{n}{A_i^2}} \sqrt{\sum\limits_{i=1}^{n}{B_i^2}} }$
Afin d’implémenter ce type de réseau dans Mariana, nous devons créer une nouvelle couche de sortie. Deux modifications sont à faire à notre nouvelle couche : 1) gérer les connections entre les couches des deux réseaux et 2) définir le calcul de notre mesure de distance, la similarité cosinus.
Commençons par définir notre nouvelle couche de sortie. Cette couche, nommée Siamese, abstrait la classe de base pour les couches de sortie de Mariana, Output_ABC.
import theano.tensor as tt
from Mariana.layers import Output_ABC
class Siamese(Output_ABC):
def __init__(self, **kwargs):
Output_ABC.__init__(self, size=1, **kwargs)
self.targets = tt.ivector(name="targets_" + self.name)
self.inpLayers = []
Une telle couche doit aussi implémenter quelques restrictions dans ses connections. Ici, la fonction _femaleConnect s’assure qu’il y ait un maximum de 2 connections en entrée et s’occupe que ces deux couches aient la même taille de sortie.
def _femaleConnect(self, layer):
if self.nbInputs is None:
self.nbInputs = layer.nbOutputs
elif self.nbInputs != layer.nbOutputs:
raise ValueError("All inputs to layer %s must have the same size, \
got: %s previous: %s" % (self.name, layer.nbOutputs, self.nbInputs))
if len(self.inpLayers) > 2:
raise ValueError("%s cannot have more than 2 input layers." % (self.name))
self.inpLayers.append(layer)
La manipulation de la sortie de la couche est décrite dans la fonction _setOutputs et implémente le calcul de la similarité cosinus.
def _setOutputs(self):
"""Defines self.outputs and self.testOutputs"""
if len(self.inpLayers) != 2:
raise ValueError("%s must have exactly 2 input layers." % (self.name))
num = tt.sum(self.inpLayers[0].outputs * self.inpLayers[1].outputs, axis=1)
d0 = tt.sqrt(tt.sum(self.inpLayers[0].outputs**2, axis=1))
d1 = tt.sqrt(tt.sum(self.inpLayers[1].outputs**2, axis=1))
num_test = tt.sum(self.inpLayers[0].testOutputs * self.inpLayers[1].testOutputs, axis=1)
d0_test = tt.sqrt(tt.sum(self.inpLayers[0].testOutputs**2, axis=1))
d1_test = tt.sqrt(tt.sum(self.inpLayers[1].testOutputs**2, axis=1))
self.outputs = num / (d0 * d1)
self.testOutputs = num_test / (d0_test * d1_test)
Et voilà! Maintenant que nous avons notre couche Siamese sous la main, passons à la construction de notre réseau.
Tout comme pour les versions antérieures de Mariana, spécifier la structure et les connections d’un réseau demeure un jeu d’enfant. Une fois instanciées, les composantes du réseau peuvent êtres reliées entre elles grâce à l’opérateur >. Ce détail permet la création rapide d’une panoplie de différentes structures telles que bifurcations, fusions et boucles (bien qu’une implémentation complète de réseaux récurrents ne soit pas encore disponible).
Notre réseau sera entraîné par descente de gradient avec un taux d’apprentissage de 0.01. L’erreur quadratique moyenne sera utilisée comme fonction de coût.
ls = MS.GradientDescent(lr=0.01)
cost = MC.MeanSquaredError()
Les couches du réseau doivent maintenant être instanciées. Deux branches, A et B, avec une couche d’entrées (_i) et deux couches cachées (_h1, _h2), sont introduites et utilisent de la rectification linéaire (MA.ReLU) comme fonction d’activation et un peu de régularisation L2 (MR.L2). La taille des couches est passée comme premier paramètre. Enfin, notre couche de sortie Siamese est instanciée et le tout est lié grâce à l’opérateur >.
import Mariana.activations as MA
import Mariana.layers as ML
import Mariana.costs as MC
import Mariana.regularizations as MR
import Mariana.scenari as MS
A_i = ML.Input(28 * 28, name='inpA')
A_h1 = ML.Hidden(28 * 28, activation=MA.ReLU(), regularizations=[MR.L2(0.01)], name='A_h1')
A_h2 = ML.Hidden(50, activation=MA.ReLU(), regularizations=[MR.L2(0.01)], name='A_h2')
B_i = ML.Input(28 * 28, name='inpB')
B_h1 = ML.Hidden(28 * 28, activation=MA.ReLU(), regularizations=[MR.L2(0.01)], name='B_h1')
B_h2 = ML.Hidden(50, activation=MA.ReLU(), regularizations=[MR.L2(0.01)], name='B_h2')
o = Siamese(learningScenario=ls, name='Siamese', costObject=cost)
network = A_i > A_h1 > A_h2 > o
network = B_i > B_h1 > B_h2 > o
Il ne nous reste maintenant qu’à lier les poids des deux branches de notre réseau. Il nous faut premièrement instancier le réseau afin que les poids subissent les mêmes initialisations.
network.init()
A_h1.W = B_h1.W
A_h2.W = B_h2.W
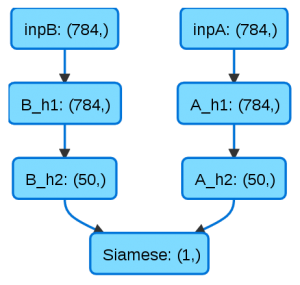
La fonction saveHTML nous offre un aperçu de la structure finale du réseau:
La version 1.0 stable de Mariana est attendue dans les prochains mois. Surveillez le compte github pour les plus récentes mises à jour!
J’aimerais souligner la contribution de Tariq Daouda, auteur de Mariana, à la rédaction de cet article.
Références
[1] Bromley, Jane, et al. « Signature verification using a “Siamese” time delay neural network. » International Journal of Pattern Recognition and Artificial Intelligence 7.04 (1993): 669-688.


Laisser un commentaire