Il arrive souvent que l’on veuille voir s’il existe une une relation quelconque entre les points d’un jeu de données. Lorsqu’il est question de régressions linéaires, celles-ci peuvent être facilement visualisées avec Seaborn, une librairie Python visant l’exploration et la visualisation plutôt que l’analyse statistique. Quant aux régressions logistiques, SciPy est un bon outil à utiliser lorsque nous n’avons pas notre propre script d’analyse.
Regardons le paquet optimisation ‘optimize’
from scipy.optimize import curve_fit
Partant de jeu de données de n paires de variables indépendantes et dépendantes (xi,yi), curve_fit utilise une approche des moindres carrés pour ajuster toute fonction f. Le cas de base ressemblera à
scipy.optimize.curve_fit(func, x, y)où x et y sont des vecteurs de données, et où func est une fonction Python retournant l’équation de la courbe à ajuster. Ce dernier argument est très intéressant puisqu’il nous donne la liberté de définir nous-mêmes une fonction modèle avec m paramètres. Curve_fit appelle leastq (une autre méthode de scipy.optimize) qui est un wrapper autour de l’algorithme Levenberg-Marquardt de MINPACK.
Par défaut, la méthode utilisée pour l’optimisation est ‘lm’ (i.e. Levenberg-Marquardt). Celle-ci est généralement la méthode la plus efficace, excepté lorsque m < n et lorsqu’il y a des contraintes sur le problème. Dans ces cas, nous devons spécifier la méthode à utiliser, c’est-à-dire ‘trf’ ou ‘dogbox’ (l’algorithme Trust Region Reflective et l’algorithme dogleg, respectivement).
scipy.optimize.curve_fit(func, x, y, method='trf')
Lorsque l’on utilise d’autres méthodes que ‘lm’, curve_fit appelle least_square plutôt que leastq. Cela étant dit, les arguments propres à leastq et à least_square peuvent tous être utilisés par curve_fit et ce, même si ceux-ci ne figurent pas dans la documentation de curve_fit. En d’autres mots, de nombreuses fonctionnalités peuvent être trouvées dans la documentation de leastq ainsi que dans celle de least_square.
Scipy.optimize.curve_fit(func, x, y) retourne un vecteur de valeurs estimées et optimales pour chacun des paramètres, ainsi qu’une matrice (vecteur 2D) de covariance des paramètres estimés. Nous pouvons facilement tracer notre courbe ajustée avec ces valeurs.
La courbe résultante pourrait ne pas être exactement ce à quoi nous nous attendions. Avant de conclure quoi que ce soit, regardons quelques arguments de curve_fit:
- f = func : il est important de s’assurer que notre équation modèle est bien écrite; l’ajout ou le retrait de parenthèses peut générer une toute nouvelle équation!
- p0 = […] : par défaut, les estimations des paramètres initiaux sont toutes égales à 1. Ces inférences peuvent très bien être éloignées des valeurs réelles, ce qui mènerait l’algorithme à converger vers de fausses valeurs optimales. Nous pouvons nous-mêmes faire l’initialisation des paramètres et ainsi essayer d’éviter ce problème (notons que nos hypothèses pourraient elles aussi être fausses).
- Dfun = dfunc : par défaut, le Jacobien de notre fonction est estimé pas MINPACK. Il est possible de le définir nous-mêmes, de façon similaire à notre func. Lorsque le jeu de données est ‘bon’, les courbes ‘estimation’ et ‘dérivé’ semblent se comporter de façon similaire (Fig. 1). Cependant, lorsque le jeu de données est ‘mauvais’, les résultats sont très différents (Fig. 2).
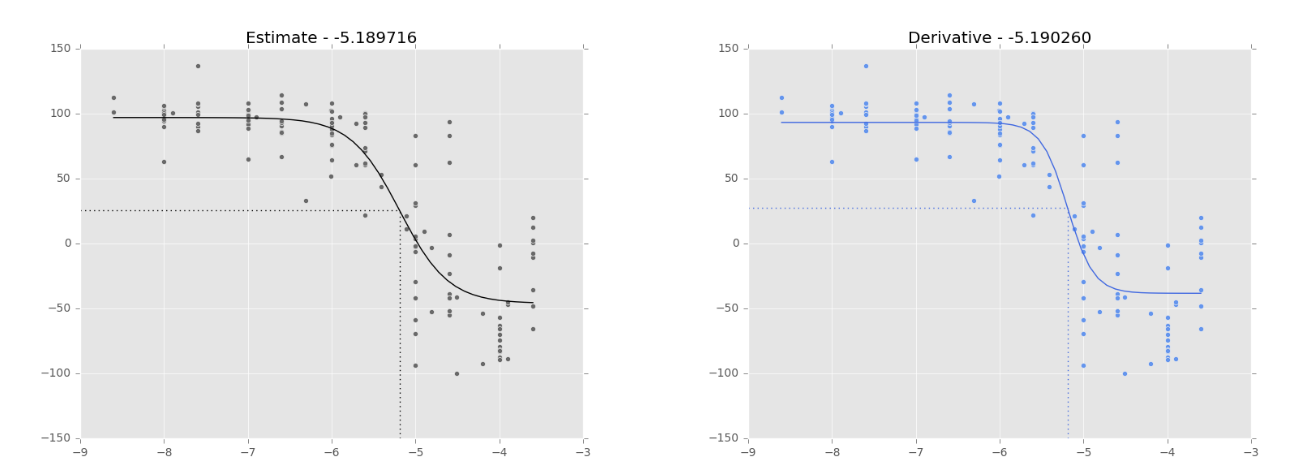
Figure 1. Régression logistique sur les données de NCI-60 (180973_Leukemia_CCRF-CEM) pour ajuster une courbe dose-réponse. Les lignes pointillées montrent le point d’inflexion, tel que calculé par SciPy.optimize.curve_fit. Sa valeur est représentée dans le titre du graphique. Courbe noire: courbe d’ajustement basée sur l’estimation du Jacobien (par défaut). Courbe bleue: courbe d’ajustement basée sur le calcul du Jacobien (Dfun = dfunc). Courbes similaires lorsque les données sont ‘bonnes’.
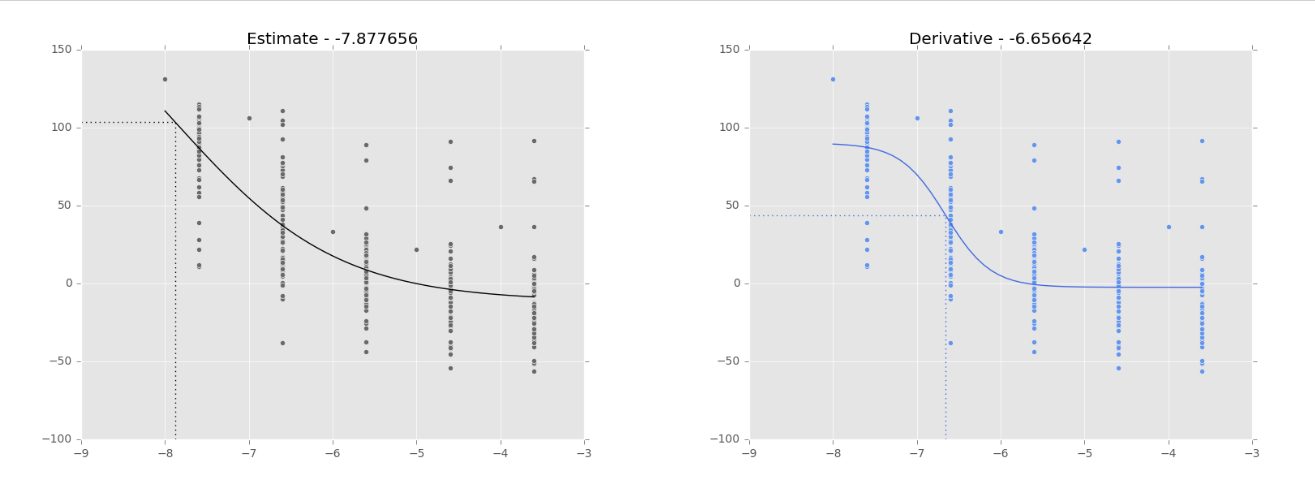
Figure 2. Régression logistique sur les données de NCI-60 (180973_Leukemia_CCRF-CEM) pour ajuster une courbe dose-réponse. Les lignes pointillées montrent le point d’inflexion, tel que calculé par SciPy.optimize.curve_fit. Sa valeur est représentée dans le titre du graphique. Courbe noire: courbe d’ajustement basée sur l’estimation du Jacobien (par défaut). Courbe bleue: courbe d’ajustement basée sur le calcul du Jacobien (Dfun = dfunc). Courbes différentes lorsque les données sont ‘mauvaises’.
SciPy est un bon outil lorsqu’il est question de régressions logistiques. Cependant, nous devrions tester différentes approches avant de tirer quelconque conclusion. Par exemple, nous pourrions comparer les moindres carrés de ‘estimation’ et de ‘dérivé’ pour voir quel est le meilleur ou si leurs résultats sont équivalents. Nous pourrions également regarder les intervalles de confiance de chaque paramètre selon en appliquant une stratégie de bootstrap.


Laisser un commentaire