Quand j’ai commencé à utiliser R, il y a une dizaine d’années, la communauté d’utilisateurs était beaucoup plus petite! Il n’y avait pas de sites comme R-bloggers pour s’inspirer ni de ggplot2 pour faire de beaux graphiques. Et c’était les débuts d’une implémentation alternative de R (autre que celle de CRAN) connue sous le nom de Revolution R de la compagnie Revolution Analytics. Revolution R tentait surtout de séduire les compagnies en offrant un R plus performant et plus rapide. Ils offraient aussi une version gratuite et accessible (open source) de leur produit appelée RRO.
En avril 2015, la compagnie a été achetée par Microsoft! Qui sait, peut-être qu’un jour, nous pourrons utiliser R dans Excel au lieu d’utiliser Visual Basics. On verra!
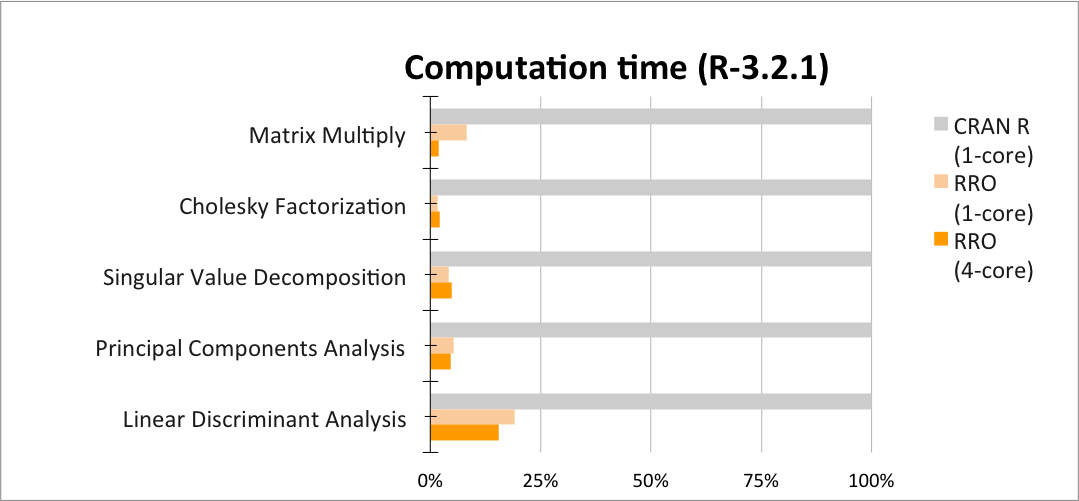
En attendant, j’ai décidé de tester RRO, maintenant renommée MRO (Microsoft R Open) pour voir si j’obtenais de meilleures performances dans le genre d’analyses que je fais quotidiennement. Un banc d’essai est disponible (résultats et code) sur le site de la compagnie pour montrer exactement quel type de gain peut être obtenu en utilisant leur implémentation parallélisée. J’ai quand même décidé de la tester, car ces opérations ne sont pas nécessairement les opérations que j’utilise le plus.
From Revolution Analytic website
J’ai donc créé mon propre petit banc d’essai. J’ai utilisé un fichier R Markdown pour que mes résultats soient joliment formatés en un document HTML (sortie en pdf ou Word est aussi possible). J’ai roulé mon banc d’essai en utilisant MRO 3.2.3 et le R 3.2.2 de CRAN. Je l’ai roulé sur mon ordinateur avec 4 coeurs. Les sortie html sont disponibles ici.
Vous vous souvenez peut-être de l’article que j’avais écrit pour mesurer quel bout de code est le plus rapide en python? On peut faire la même chose en R!
Il y a deux fonctions simples pour mesurer le temps que prend un bout de code ou une fonction : proc.time() et code>system.time(). Vous pouvez les utiliser comme ceci :
# Principal Component Analysis
m <- 10000
n <- 2000
A <- matrix (runif (m*n),m,n)
system.time (P <- prcomp(A))
## or
ptm <- proc.time()
P <- prcomp(A)
proc.time() - ptm
# user system elapsed
# 122.594 1.122 123.583
#The ‘user time’ is the CPU time charged for the execution of user instructions of the calling process.
#The ‘system time’ is the CPU time charged for execution by the system on behalf of the calling process.Toutefois, nous voulons parfois récupérer un peu plus de détails pour identifier les étapes qui prennent le plus de temps. Le package R timeit nous permet de faire cela facilement. timeit est en fait un profileur (profiler). On l'utilise de la même façon que pour system.time .
t0 <- timeit (P <- prcomp(A), replications=1, times=1)
# self.time self.pct total.time total.pct mem.total replications iteration
# "La.svd" 98.34 78.994296731 98.65 28.320032152 488.4 1 1
# "%*%" 25.27 20.298819182 25.27 7.254406614 152.6 1 1
# "matrix" 0.23 0.184753795 0.23 0.066027444 183.1 1 1
# "array" 0.16 0.128524379 0.16 0.045932135 152.6 1 1
# "aperm.default" 0.14 0.112458832 0.14 0.040190618 152.6 1 1
# "is.finite" 0.11 0.088360511 0.11 0.031578343 152.6 1 1
# "colMeans" 0.08 0.064262190 0.08 0.022966068 0.0 1 1
# "svd" 0.05 0.040163869 98.81 28.365964288 671.5 1 1
# "any" 0.04 0.032131095 0.04 0.011483034 0.0 1 1
# "t.default" 0.03 0.024098321 0.03 0.008612275 30.5 1 1
# "sweep" 0.02 0.016065547 0.32 0.091864271 305.2 1 1
# "prcomp.default" 0.01 0.008032774 124.49 35.738071999 1159.9 1 1
# "as.matrix" 0.01 0.008032774 0.01 0.002870758 0.0 1 1
Les deux premières colonnes sont celles qui nous intéressent. self.time et self.pct présentent respectivement le temps en secondes et le pourcentage du temps total que prend l'exécution du code défini en rangée.
Dans ma sortie, vous pouvez voir toutes les étapes requises par une analyse en composantes principles et le temps et la mémoire qu'elles utilisent. Pour étudier du code s'exécutant très rapidement, les paramètres "replications" et "iteration" sont très utiles. Dans la sortie présentée plus haut, on peut voir que prcomp utilisent les fonctions any et as.matrix et qu'elles s'exécutent très rapidement contrairement à %*% et La.svd qui sont plus coûteuses. Pour connaître le temps d'exécution total, nous pouvons faire la somme de la colonne self.time column.
sum(t0$self.time)
#123.51
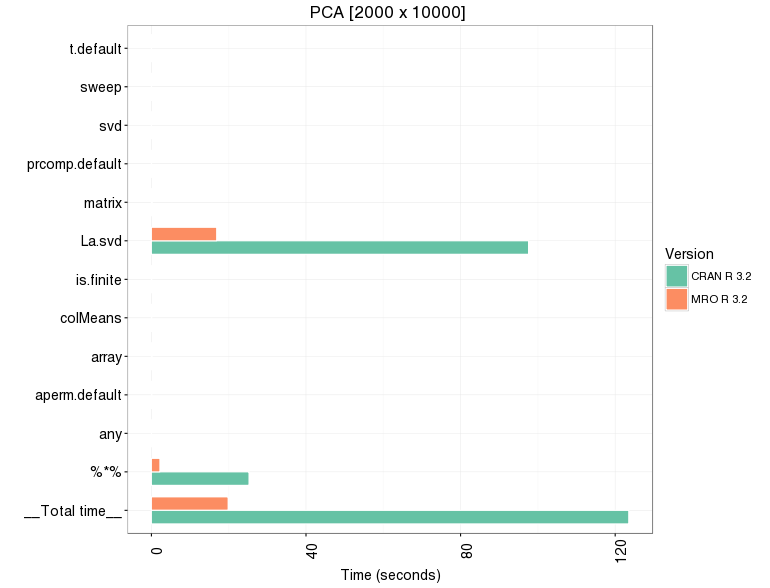
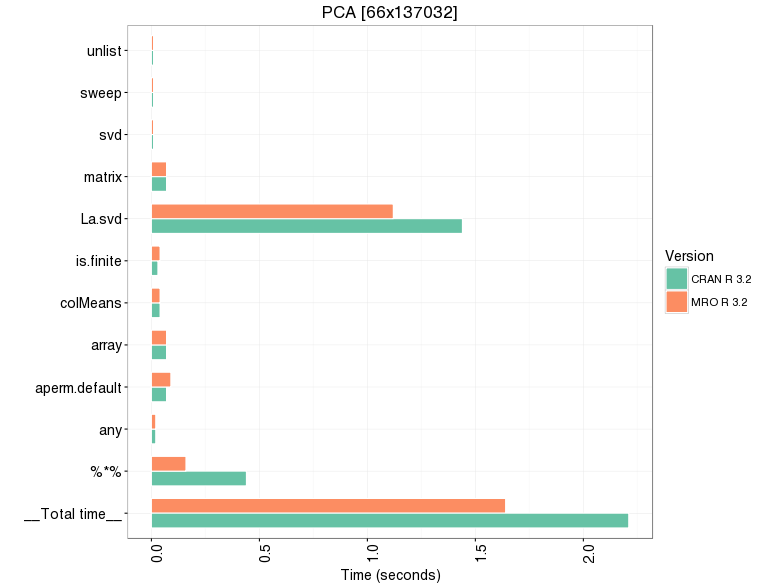
Voici quelques résultats que j'ai obtenus. J'ai d'abord utilisé l'exemple pour la PCA fourni sur le site de Revolution Analytics; PCA sur une matrice de 2000 x 10000. Dans ce cas-ci, MRO est clairement plus rapide (27.8 vs 129.3 secondes!!). C'était un peu moins clair lorsque j'ai fait la PCA sur mes propres données (66 x 137032) qui comportaient seulement 66 rangées au lieu de 2000 (2.02 vs 2.26 secondes). Pour les autres opérations, elles bénéficient peu d'une implémentation en parallèle. En fait, selon les gens de MRO, la régression linéaire, le produit vectoriel tout comme le calcul du déterminant et la décomposition de Cholesky sont des opérations qui bénéficient beaucoup de l'utilisation d'opérations parallélisées. Comme on peut s'y attendre, la création/manipulation/transformation de matrices tout comme les boucles et la récursion ne profitent d'aucun gain. Ce sont des opérations qui ne sont pas vraiment parallélisables.
| Task | Time (seconds) CRAN R |
Time (seconds) MRO |
|---|---|---|
| PCA [2000x10000]- MRO example- |
123.51 | 19.85 |
| PCA [66x137032] | 2.26 | 2.02 |
| PCA - transposed matrix | 2.94 | 5.56 |
| apply(2, as.numeric) | 0.29 | 0.32 |
| matrix construction (with an if statement) -rbind | 1.43 | 1.64 |
| matrix construction (with an if statement) -assignment | 1.03 | 1.12 |
 |
 |
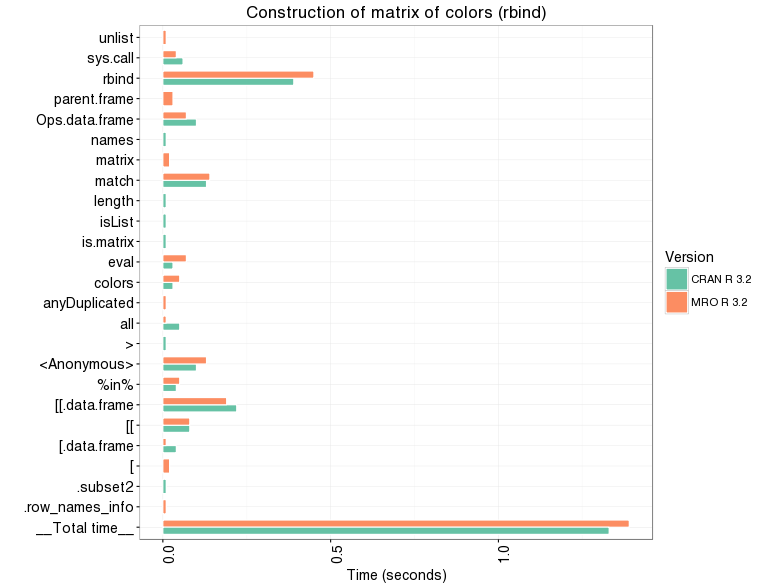
Un fait intéressant, avec le profileur, nous pouvons voir que construire une matrice en utilisant une boucle for, rbind et une condition (bleu pour les valeurs plus grandes que 4 par exemple, sinon noir) n'implique pas les mêmes fonctions internes selon l'implémentation utilisée.


Laisser un commentaire