Toutes les expériences d’expression génique sont influencées par plusieurs variables. Il y a celle qui nous intéresse (la variable d’intérêt) et…les autres. Ces autres variables (d’origine technique ou biologique), introduisent de la variabilité dans les données. Et elle passe souvent inaperçue.
Prenons une expérience où nous voulons étudier comment un traitement affecte l’expression des gènes. Le traitement est donc la variable d’intérêt et elle est au coeur de l’expérience. Mais toutes différences dans les instruments utilisés, dans la façon de manipuler les échantillons, dans le background génétique, dans l’âge des patients peuvent aussi influencer l’expression des gènes. Il est donc très fréquent d’observer des effets de batch dans ce type de jeux de données.
Les effets de batch peuvent affecter les gènes qui sont associés à la variable d’intérêt ou non. Par exemple, l’expression d’un gène donné peut être influencée par l’âge du patient en plus d’être influencée par le traitement étudié. C’est un problème, car ignorer les effets de batch peut mener à des conclusions biologiques fautives.
Ceci est particulièrement vrai si l’effet de batch est corrélé avec la variable d’intérêt. Par exemple, supposons que vous vouliez étudier l’effet d’un traitement et que vous séquenciez tous vos échantillons « contrôle » le même jour et tous les échantillons « traitement » une semaine plus tard. Dans un monde idéal, il n’y aurait pas de différences dans les résultats obtenus à ces deux dates autres que celles liées à la réponse au traitement. Mais si quelque chose arrive (un bris de climatisation, un nouveau lot de réactif, un oubli, etc), distinguer l’effet du traitement de la variation technique sera très difficile avec un tel design expérimental. Vous pourriez penser, par exemple, que le traitement active une voie de signalisation en lien avec la réponse au stress alors que cela serait plutôt dû à une différence dans les conditions de manipulation des échantillons. Rappelez-vous, corrélation n’est pas synonyme de causalité.
Pour éviter ce genre de situation, il faut planifier son expérience au préalable avec soin. Il faut réduire le plus possible les sources de variation et bien balancer la variabilité qu’on ne peut pas contrôler afin d’éviter les variables confondantes. Surtout n’hésitez pas à consulter un bio-statisticien ou un bio-informaticien AVANT de faire l’expérience.
Analyse SVA (surrogate variable analysis)
Malgré toutes les précautions, il arrive parfois que nous ayons à travailler avec des données bruitées. Parmi les méthodes existantes pour corriger les effets de batch, certaines assument que les effets sont connus tandis que d’autres tentent de les découvrir. Dans le premier cas, on prendra donc en compte la variable connue dans l’analyse. Dans le deuxième cas, on tentera d’identifier la variabilité « inconnue » pour ensuite la contrôler. C’est dans la deuxième catégorie qu’entre SVA (surrogate variable analysis). SVA tente d’identifier la variabilité « inconnue » et essaie de la contrôler en construisant des variables qui peuvent ensuite être utilisées dans les analyses subséquentes (dans des modèles linéaires par exemple).
La méthode a été développée en 2007 par Leek et al pour analyser les effets de batch dans les biopuces (microarrays). L’algorithme a évolué depuis la publication originale (Leek et al. 2008, Leek et al, 2012) et il existe aujourd’hui plus d’une version pouvant être utilisées selon le contexte et les données (svaseq pour des données de séquençage, supervised sva, frozen sva lorsqu’on a un ensemble d’entrainement et de test). La méthode est couramment utilisée pour corriger les effets de batch et est disponible dans la librairie R de Bioconductor sva ainsi que dans d’autres librairies comme limma. À noter que SVA n’est pas approprié dans tous les contextes, particulièrement si la question d’intérêt implique des groupes composés de plusieurs sous-groupes hétérogènes.
Bien qu’il existe plusieurs implémentations, l’idée de base reste la même : 1) enlever le signal attribué à la variable d’intérêt (rappelez-vous que l’on veut identifier de la variabilité « inconnue ») et identifier un sous-groupe de gènes affectés par la variabilité restante, 2) décomposer la matrice d’expression ainsi réduite pour construire des variables de substitution, 3) utiliser ces variables de substitution dans les analyses subséquentes comme des variables « connues ».
Pour arriver à cela, SVA utilise deux méthodes plutôt intéressantes : les modèles linéaires et la décomposition. Mon but ici n’est pas d’expliquer en détail comment SVA fonctionne, mais plutôt de vous introduire à ces deux approches.
Modèles linéaires et décomposition
Modèles linéaires
Avec les modèles linéaires, le but est d’estimer les paramètres d’une équation, généralement de la forme suivante :
Yi = β0 + β1xi + ei
Les coefficients β sont estimés en minimisant l’erreur entre les points (Yi) et la sortie de l’équation pour les xi correspondants. Dans le contexte de l’expression génique, nous assumons que l’expression est composée de différents signaux : la valeur de base, l’effet lié à la condition biologique étudiée, l’effet lié aux autres variables connues, l’effet lié aux batch « inconnues » et l’erreur.
expression_gene = expression_de_base + effet_biologique + effet_batch_connue + effet_batch_inconnue + erreur
Il est ainsi possible d’estimer la contribution de chaque variable à l’expression d’un gène. Par exemple, on peut estimer quelle est la contribution (effet) de la variable biologique dans l’expression. Pour des exemples pratiques, je vous conseille de regarder le manuel d’utilisation de la librairie limma.
Décomposition en valeurs singulières (Singular value decomposition)
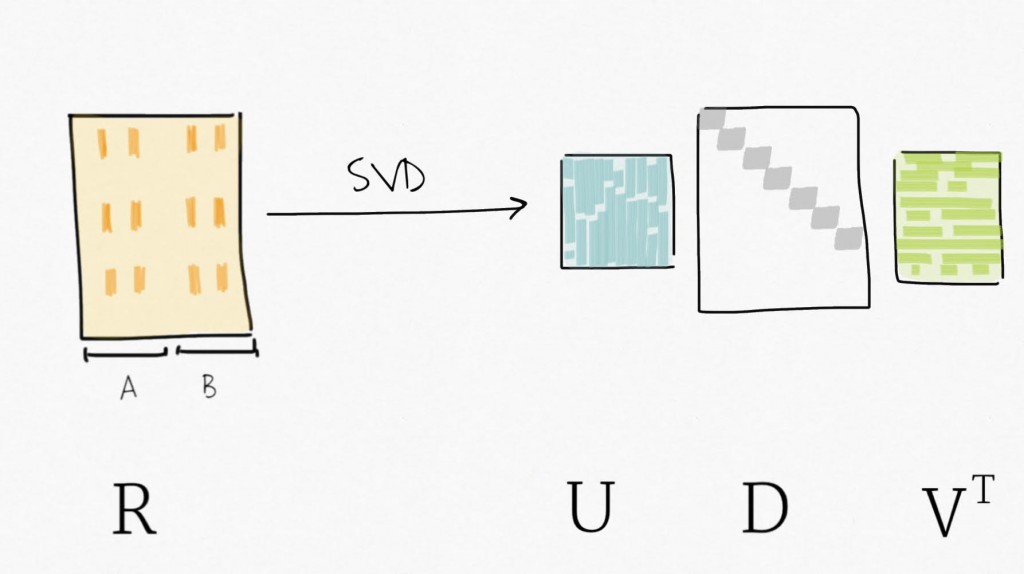
La décomposition en valeurs singulières (SVD) peut être vue comme une technique de réduction du nombre de dimensions. SVD décompose une matrice en trois matrices : Y=UDV⊤ . Plus précisément, pour une matrice Y de taille m x n , SVD décompose Y en une matrice orthogonale U de taille m x p, en une matrice orthogonale V de taille p x p et en une matrice diagonale D de taille n x p pour p=min(m,n). SVD fournit un moyen de compresser des données en un nombre réduit de variables triées, les premières variables expliquant une plus grande proportion de la variance (de la variabilité) que les suivantes. C’est similaire à l’analyse en composantes principales (PCA).
Mais comment tout cela est-il lié à SVA?
Pour soustraire le signal attribué à la variable biologique d’intérêt, SVA ajuste un modèle linéaire qui ne contient que cette variable. Le signal associé à cette variable est estimé et retiré des données pour créer une matrice d’expression résiduelle. N’oubliez pas, l’idée est de récupérer des variables de substitution représentatives de la variabilité inconnue, et non de la variabilité associée à la variable d’intérêt.
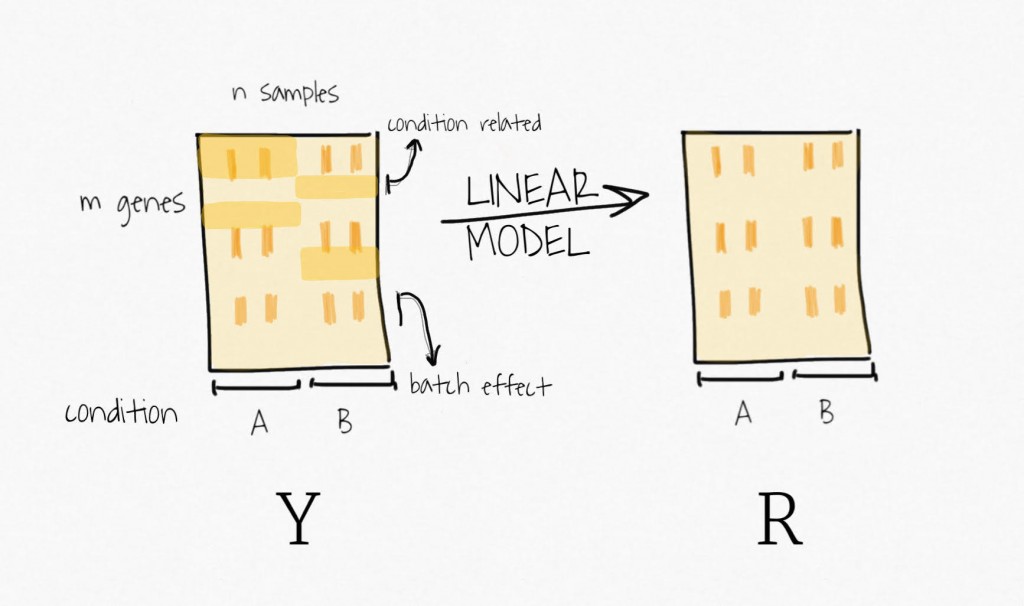
Ensuite, la décomposition de la matrice d’expression résiduelle par SVD permet d’obtenir un ensemble de variables ordonnées par variabilité expliquée décroissante.
Ces variables « compressées » sont utilisées pour identifier des sous-groupes de gènes associés à la variabilité capturée. Considérez les sous-ensembles de gènes comme des signatures dans l’expression résiduelle. Les sous-groupes sont utilisés pour créer des matrices d’expression réduites.
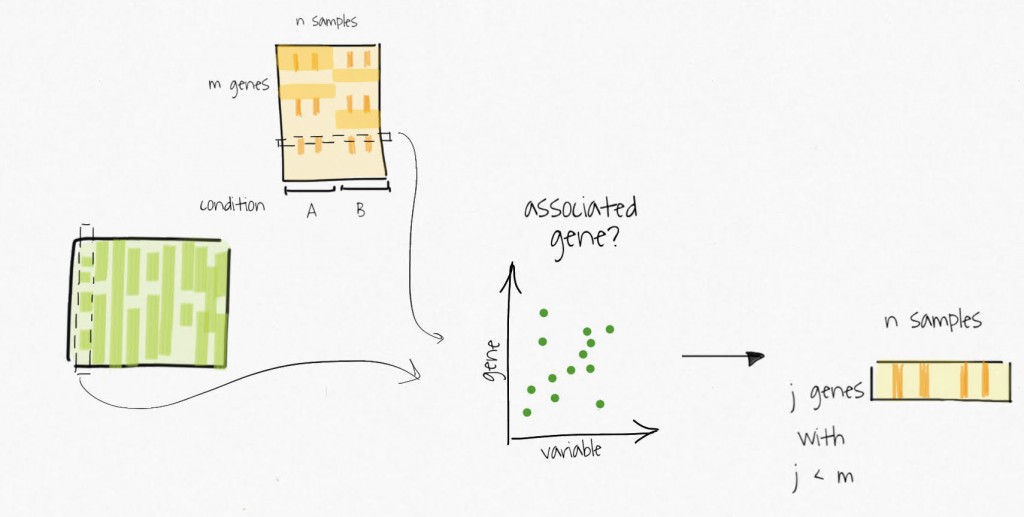
La décomposition par SVD des matrices d’expression réduites fournit des estimés des variables de substitution. Ces dernières peuvent ensuite être utilisées dans les analyses subséquentes.
Quelques petites notes ici, les variables de substitution représentent collectivement la variabilité inconnue, elles ne seront pas nécessairement associées à une source de variation spécifique. Il n’y aura pas nécessairement une variable qui sera représentative de l’instrument utilisé par exemple. Aussi, notez que les figures ci-dessus ne visent qu’à rendre les choses plus claires et ne sont pas complètes ou exactes. Pour tous les détails, il vaut mieux consulter la description des algorithmes dans les papiers cités.
En terminant, je ne peux pas me prononcer à savoir si SVA est la meilleure approche pour corriger les effets de batch. Mais j’espère que l’explication des concepts utilisés vous donnera une meilleure compréhension de la correction d’effet de batch (et de bruit) en général.


Laisser un commentaire