En 2016, Bray et al. ont introduit une nouvelle méthode basée sur les k-mers pour estimer l’abondance des isoformes dans les données de RNA-Seq. La méthode s’appelle kallisto. Comparée aux méthodes existantes, pour une précision de résultat comparable, kallisto est plus rapide et plus efficace en mémoire ce qui constitue une amélioration significative. En fait, kallisto est capable de quantifier l’expression d’un échantillon en l’espace d’une vingtaine de minutes au lieu de prendre plusieurs heures. Comme cette méthode est légère et conviviale, elle est de plus en plus utilisée pour quantifier l’expression sous forme de TPM. Mais comment fonctionne-t-elle?
Les méthodes standards (précédentes) utilisées pour la quantification de l’expression reposent sur une étape d’alignement, c’est-à-dire sur l’alignement des reads séquencés par RNA-Seq à un génome de référence. Les reads sont assignés à une position sur le génome de référence et les valeurs d’expression pour les gènes ou les isoformes sont dérivées en comptant le nombre de reads chevauchant ces derniers.
L’idée derrière kallisto est de se baser sur un pseudo-alignement qui ne nécessite pas d’alignement (de connaître la position exacte d’un read dans un transcrit) à une séquence. L’idée est de seulement récupérer le transcript d’origine potentiel. Ainsi, kallisto évite de faire l’alignement de chaque read à un génome de référence ce qui constitue une étape très coûteuse. En fait, il n’utilise même pas le génome de référence, seulement une collection des séquences du transcriptome.
Avant de pouvoir analyser des échantillons séquencés, il faut construire l’index kallisto. Kallisto construit d’abord un graphe de Bruijn (T-DBG) « colored » à partir de tous les k-mers trouvés dans le transcriptome.
Chaque noeud du graphe correspond à un k-mer (une courte séquence de k bases) et contient l’information de son origine (de quel transcrit il peut venir) sous forme de couleur. Les tracés linéaires de même couleur dans le graphe correspondent aux transcrits ou aux contigs. Une fois le T-DBG construit, kallisto conserve le lien entre chaque k-mer et son ou ses transcrit(s) d’origine de même que sa position dans le(s) transcrit(s). Cette étape n’est exécutée qu’une seule fois et est dépendante d’un fichier d’annotation qui doit être fourni.
Ensuite, pour un échantillon séquencé donné, kallisto décompose chaque reads en ses k-mers et utilise ces k-mers pour trouver un chemin couvrant (path covering) dans le graphe T-DBG. Ce chemin dans le graphe du transcriptome, où un chemin correspond à un transcrit, génère des classes de k-compatibilité pour chaque k-mer, c’est-à-dire un ensemble de transcrits d’origine potentiel associé à un noeud. Les transcrits d’origine potentiel pour un read (pas un k-mer ici) peuvent être obtenus en faisant l’intersection des classes de k-compatibilité de ses k-mers. Pour que le pseudoalignement soit plus rapide, kallisto ne regarde pas les k-mers redondants puisque les k-mers voisins appartiennent souvent au même transcrit. La Figure1, qui provient de l’article, résume les différentes étapes (petite note, je n’ai pas traduit la légende de la figure).
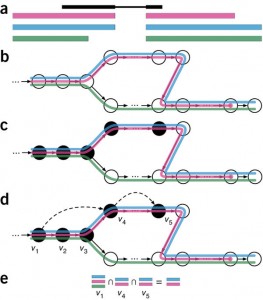
Figure1. Overview of kallisto. The input consists of a reference transcriptome and reads from an RNA-seq experiment. (a) An example of a read (in black) and three overlapping transcripts with exonic regions as shown. (b) An index is constructed by creating the transcriptome de Bruijn Graph (T-DBG) where nodes (v1, v2, v3, … ) are k-mers, each transcript corresponds to a colored path as shown and the path cover of the transcriptome induces a k-compatibility class for each k-mer. (c) Conceptually, the k-mers of a read are hashed (black nodes) to find the k-compatibility class of a read. (d) Skipping (black dashed lines) uses the information stored in the T-DBG to skip k-mers that are redundant because they have the same k-compatibility class. (e) The k-compatibility class of the read is determined by taking the intersection of the k-compatibility classes of its constituent k-mers. [Figure tirée de Bray et al. Near-optimal probalistic RNA-seq quantification, Nature Biotechnology, 2016.]
Ensuite, kallisto optimise la fonction de vraisemblance du RNA-Seq en utilisant l’agorithme « expectation-maximization » (EM).
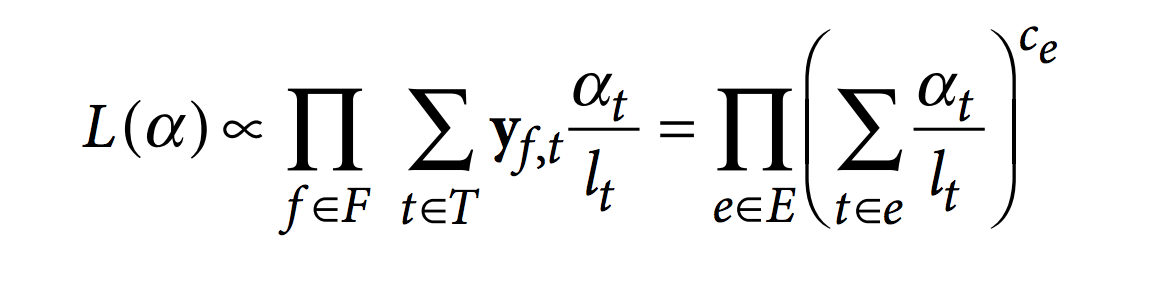
Dans cette fonction, F est l’ensemble des fragments (ou reads), T est l’ensemble des transcrits, lt est la longueur (effective) du transcrit t et yf,t est la matrice de compatibilité définie comme 1 si le fragment f est compatible avec t et 0 sinon. Les paramètres αt sont les probabilités de sélectionner des reads provenant du transcrit t. Ces αt sont les paramètres d’intérêt puisqu’ils représentent l’abondance des isoformes ou l’expression relative.
Pour rendre l’algorithme plus rapide, la matrice de compatibilité est « factorisée » en classes d’équivalence. Une classe d’équivalence consiste en tous les reads compatibles ayant le même sous-ensemble de transcrits. L’algorithme EM est appliqué sur les classes d’équivalence et non sur les reads. Chaque αt est optimisé pour maximiser la vraisemblance.
Nous pouvons illustrer les différentes étapes impliquées dans kallisto avec un petit exemple. En partant d’un minuscule génome de 3 transcrits, nous assumons que notre expérience de RNA-Seq a produit 4 reads comme le montre l’image suivante.
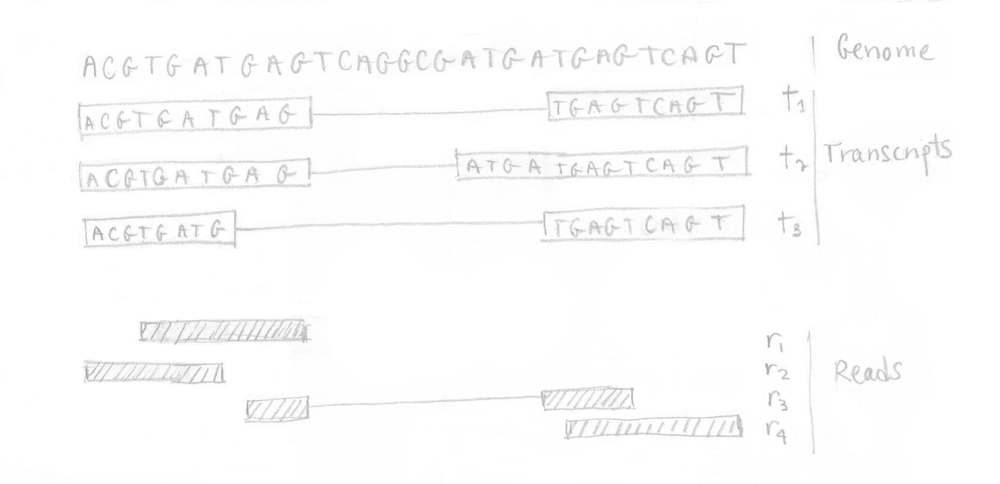
Si vous vous rappelez bien, la première étape était la construction du graphe T-DBG et de l’index de kallisto. Toutes les séquences des transcrits sont décomposées en k-mers (ici k=5) pour construire le graphe de Bruijn. Je n’ai pas représenté tous les noeuds/k-mers dans mon dessin mais vous pouvez imaginez des noeuds alignés (sans branchement) et des noeuds qui branchent représentant différents transcrits. L’idée est que chaque transcrit différent produira un chemin différent dans le graphe. Le brin n’est pas considéré ici.
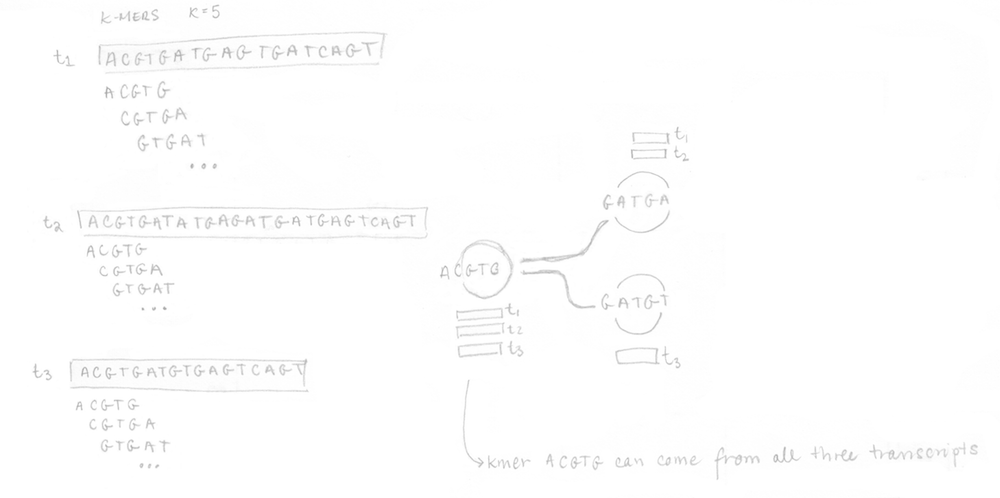
Une fois l’index bâti, les 4 reads de l’échantillon séquencé peuvent être analysés. Ils sont décomposés en k-mers (k=5 ici aussi) et l’index pré-construit est utilisé pour déterminer les classes de k-compatibilité de chaque k-mer. Ensuite, la classe de k-compatibilité de chaque read est déterminée en regardant l’intersection. Par exemple, pour le read 1, l’intersection de toutes les classes de k-compatibilité de ses k-mers suggère qu’il pourrait provenir du transcrit 1 ou 2.
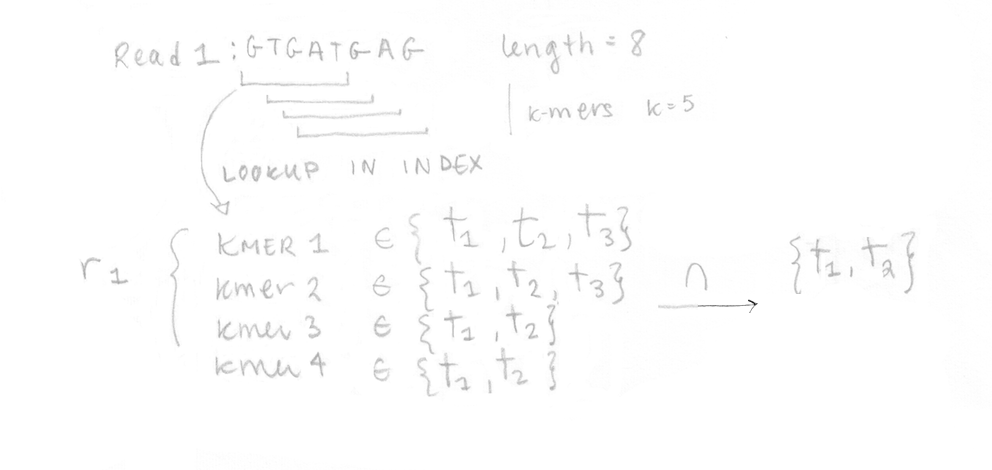
Ceci est fait pour les quatre reads ce qui nous permet de construire la matrice de compatibilité yf,t qui se trouve dans l’équation de la function de vraisemblance pour le RNA-Seq que nous voulons maximiser. J’ai réécrit les différentes parties de l’équation avec quelques explications. Dans notre cas, appliquer l’algorithme EM à 4 reads n’aurait pas été trop long, mais en réalité, l’appliquer à des millions de reads serait très lent.
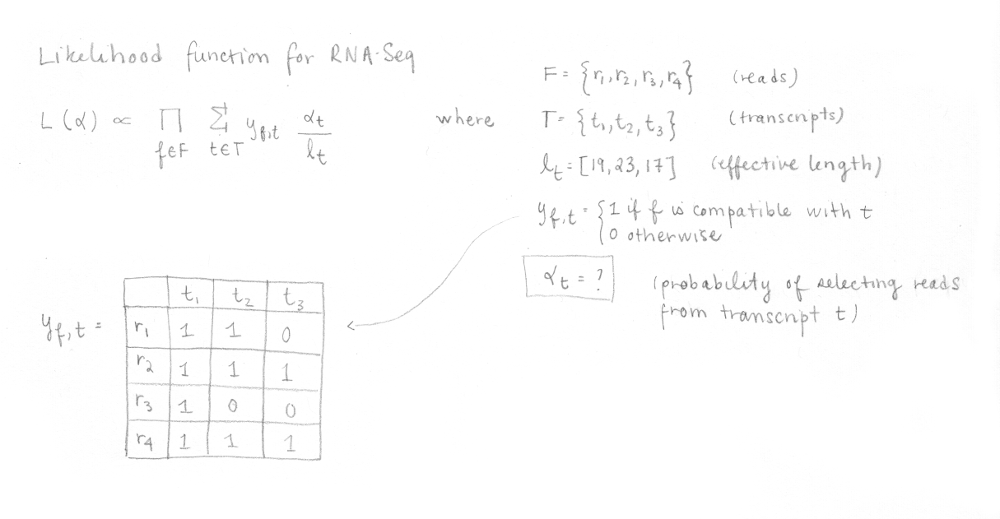
Pour raccourcir le temps d’exécution, la matrice de compatibilité yf,t est transformée en ses classes équivalentes et un compte est calculé pour chacune des classes (combien de reads sont représentés par cette classe). L’algorithme EM utilise cette information pour maximiser la nouvelle, mais équivalente, fonction de vraisemblance pour le RNA-Seq afin d’optimiser les αt , qui sont les valeurs que nous voulons déterminer.

L’algorithme EM changera αt pour maximiser L(α), i.e. il essaiera différentes valeurs de probabilités pour chaque transcrit dans le but d’avoir la plus grande vraisemblance possible. Et il fait cela intelligemment, d’une façon qui lui permet de converger. Je n’ai pas roulé l’algorithme EM, mais pour se donner une idée intuitive, regardons un petit exemple. Dans cet exemple, j’ai initialisé les trois probabilités αt (i.e. probabilité de sélectionner des reads provenant de chacun des transcrits) à une valeur de to 0.33 pour les 3, ce qui donne une vraisemblance, L(α), de 8.4e-05.
Si je change les valeurs d’abondance pour [0.98, 0.01, 0.01] (plus de chance de venir du transcrit 1) au lieu de [0.33, 0.33, 0.33], j’obtiens maintenant une L(α) de 4.2e-4, ce qui est supérieur à 8.4e-05. [0.05, 0.05, 0.9] donne 2.2e-06. Vous comprenez l’idée….
[0.33, 0.33, 0.33] ==> 8.4e-05
[0.45, 0.15, 0.4] ==> 0.00011
[0.98, 0.01, 0.01] ==> 0.00042
[0.9, 0.05, 0.05] ==> 0.00037
[0.05, 0.9, 0.05] ==> 1.5e-05
[0.05, 0.05, 0.9] ==> 2.2e-06
[0.15, 0.45, 0.4] == >3.3e-05
En considérant cet exemple de 4 reads, il est probable que les reads proviennent du transcript 1 qui serait le transcrit le plus abondant des trois transcrits. On pourrait donc dire que les transcrits 1,2 et 3 ont respectivement une abondance de 0.98, 0.01, et 0.01. Dans kallisto, l’algorithme EM s’arrête lorsque pour chaque transcrit t, αtN > 0.01, où N est le nombre total de reads, change de moins de 1%.
Quoique ce soit un article très intéressant, l’article décrivant kallisto n’est pas super facile à comprendre. J’espère avoir un peu démystifié comment fonctionne cet outil de plus en plus utilisé.


Laisser un commentaire