GEO est une source extrêmement riche de données de profils transcriptionnels, mais télécharger et préparer ces données constituent bien souvent un obstacle pour les apprentis bioinformaticiens. La démonstration qui suit devrait faciliter vos premiers pas, j’utiliserai le jeu de données de Leucégène. Une fois ces données chargées et prêtes à être utilisées dans R, je présenterai une perspective simplifiée mais pratique de l’utilisation de la PCA (Principal Component Analysis) pour faire de l’analyse exploratoire d’un ensemble de profiles transcriptionnels.
Chargement des données
Un jeu de données de 285 profils d’expression de leucémie myéloïde aiguë (LMA) peut être téléchargé de GEO à cette adresse (Accession: GSE67040). Cette cohorte a été séquencée (RNA-Seq) dans le cadre du projet Leucégène (site web) et représente 285 patients. Une fois téléchargé de GEO, le fichier « GSE67040_RAW.tar » peut être « détaré » sur Mac en double cliquant dessus (sur linux, vous pouvez utiliser la commande « tar xvf GSE67040_RAW.tar »). Cela générera 285 fichiers .txt, chacun contenant l’expression de 24 553 gènes. Les fichiers ressembleront à ceci:
chr1 11874 14361 DDX11L1 0.04970 1400
chr1 14410 29370 WASH7P 1.95957 59227
chr1 69091 70008 OR4F5 0.00620 100
chr1 134773 140566 LOC729737 2.24401 215729
chr1 567705 567793 MIR6723 0.00000 0
Pour charger un seul fichier en R, vous pouvez utiliser:
data <- read.delim ("GSM1636929_14H038_RPKM.txt", header=F, col.names=c("chr", "start", "end", "sym", "rpkm", "count"))
head (data)
chr start end sym rpkm count
1 chr1 11874 14361 DDX11L1 0.04970 1400
2 chr1 14410 29370 WASH7P 1.95957 59227
3 chr1 69091 70008 OR4F5 0.00620 100
4 chr1 134773 140566 LOC729737 2.24401 215729
Pour charger tous les fichiers, nous devons boucler à travers les noms de fichier contenant un motif donné (« GSM.*_RPKM ») et concaténer les résultats dans un data frame. Il ne faut pas oublier d’ajouter une colonne pour identifier l’échantillon pour lequel les valeurs d’expression ont été mesurées. Les quelques lignes de code suivantes prendront 5 à 10 minutes à s’exécuter (la fonction « rbind » est plutôt lente. Le code pourrait être optimisé, mais je laisse cette tâche aux lecteurs plus curieux!) :
all.fn <- list.files (pattern="GSM.*_RPKM.txt")
all.data <- data.frame()
data.len <- sapply (all.fn, function (fn) {
pat <- unlist (strsplit (fn, "_"))[2] ## Extraction de l'identificateur patient
data <- read.delim (fn, header=F, col.names=c("chr", "start", "end", "sym", "rpkm", "count"))
data$pat <- pat ## Ajout d'une colonne identifiant le patient
all.data <<- rbind (all.data, data) ## Ajout des différents profils dans all.data
nrow (data) ## Pour vérifier que les profils contiennent le même nombre de gènes, voir data.len
}Les données dans all.data sont présentées dans un format que l’on appelle « long »: chaque rangée représente une seule valeur d’expression et les premières colonnes servent à identifier le gène. Ici, nous combinerons les colonnes #1-4 et utiliserons le résultat comme nom de gène, nous conserverons la colonne #5 pour l’expression (mesurée en RPKM). Pour les utilisateurs de l’excellent package de graphiques ggplot2, vous aurez reconnu que ce format long correspond à la forme préférée par le package. Ce format est aussi très utile lorsque l’on travaille avec les fonctions « lm » et « glm »! Toutefois, nous préférons ici travailler avec un format de matrice plus traditionnel où nous avons les gènes en rangées et les patients en colonnes. Je convertirai donc mes données du format long au format « large » (wide). Cela se fait facilement avec la fonction « acast » du package « reshape2 » (le package reshape offre des fonctions pour effectuer des conversions des formats long à large et de large à long). Finalement, je transformerai les RPKM en utilisant une transformation « started-log » (introduite par J. Tuckey en 1957!).
library (reshape2)
z <- acast (all.data, chr + start + sym ~ pat, value.var="rpkm")
zl <- log10 (z + 0.001)Analyse en composantes principales (PCA)
Les données sont chargées et sont prêtes à être analysées… mais par où commencer? C’est une bonne habitude de prendre un peu de temps pour explorer les données. Un bon outil à appliquer aux données pour cela est la PCA. Il existe un grand nombre de références expliquant les bases mathématiques de cette méthode (pour les lecteurs curieux, je vous réfère à la présentation exhaustive de Jolliffe 1986). Pour ma part, j’aime penser à la PCA comme une méthode pour définir une série de signatures de gènes dans lesquelles à chaque gène correspond un poids lui conférant une importance spécifique dans une signature donnée.
La première signature (appelée première composante dans le jargon de la PCA ou PC1 dans R) identifie les gènes qui peuvent le mieux différencier les échantillons du jeu de données. Si l’on prend chaque profil transcriptionnel et qu’on multiplie l’expression des gènes par les poids donnés par la première composante et qu’on fait la somme du résultat pour obtenir un score unique, ce score représentera le maximum de variance qu’il est possible de représenter par une seule valeur. Le seconde composante (ou signature) sera orthogonale à la première, c’est-à-dire qu’elle capturera des variations qui sont indépendantes de celles capturées par la première composante. Et ainsi de suite pour les autres composantes.
En utilisant la PCA, nous remplacerons ainsi chaque profil transcriptionnel (24 553 expressions par échantillon) par un ensemble de valeurs (les scores dont il était question plus haut) qui préservent les variations observées dans le jeu de données complet.
pr <- prcomp (t (zl), center=T)
x <- predict (pr)La variable « pr$rotation » contient les signatures (composantes), une par colonne, et la fonction « predict » est utilisée pour calculer les « scores » de ces signatures pour chacun de nos échantillons.
plot (x[,c(1,2)], pch=20)
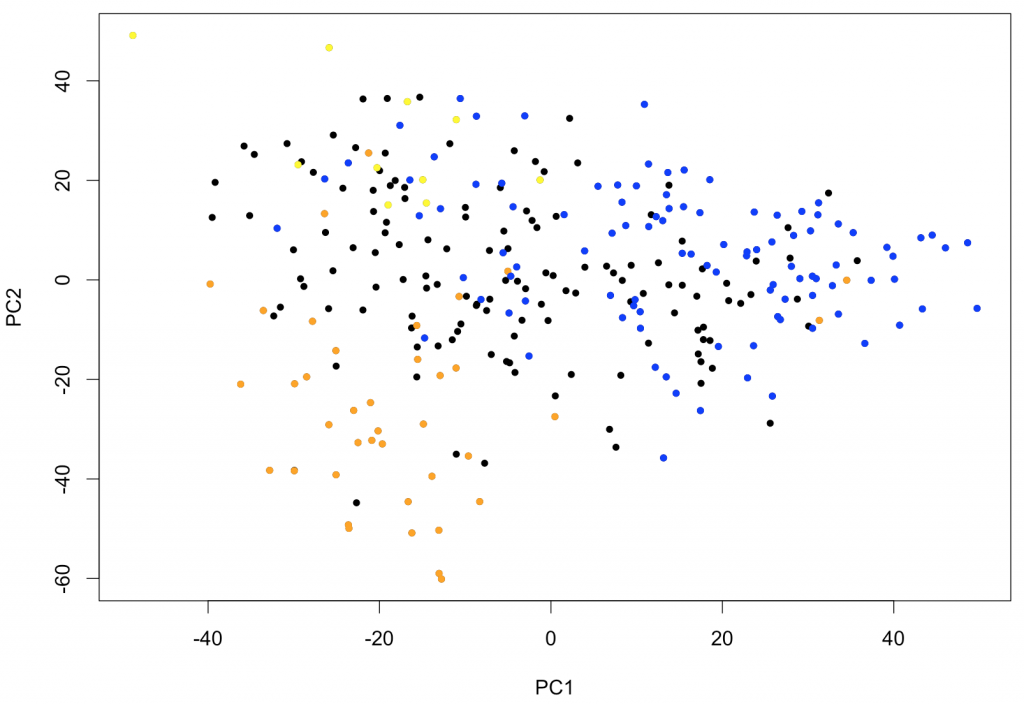
text (x[,c(1,2)], rownames (x))Avec ce type de représentation, il est très facile d’identifier des valeurs extrêmes (outliers) dans un jeu de donnée de grande dimensionalité. Si des échantillons forment des groupes facilement identifiables, ils deviendraient aussi apparents. Le code suivant illustre comment la PCA peut être utile comme première étape exploratoire. Il est possible d’identifier les échantillons de leucémie appartenant aux classes FAB M0-1 (M0 et M1 combinées), M5 et M6. Ces types de leucémie sont reconnus pour leur profil d’expression caractéristique. La sortie de la PCA montre clairement que la PC1 (la « signature » principale identifiée par la PCA) permet d’identifier les M0-1 et que la PC2 permet de distinguer les M5 des M6.
p.M6 <- scan (what=character())
04H017 04H039 05H097 07H024 10H066 11H183 07H034 03H028 12H067 12H117
p.M5 <- scan (what=character ())
03H041 07H089 07H134 08H089 10H026 12H096 14H031 01H001 02H026 02H032 02H033 03H016 03H067 04H080 04H111 04H115 04H118 04H121 05H025 05H065 05H128 05H143 06H010 06H016 06H073 06H074 07H041 07H045 07H063 08H011 08H021 08H063 08H108 08H139 09H008 09H010 09H024 09H032 09H098 09H102 10H022 10H055 10H058 10H127 11H006 11H083 11H095 11H192 13H019 13H141 13H185 03H052 04H041 05H013 05H094 05H181 07H055 07H155 08H004 08H049 08H104 09H042 09H106 09H111 10H029 10H031 10H072 10H161 11H126
p.M01 <- scan (what=character ())
02H003 02H017 03H030 04H096 05H179 06H133 06H135 07H038 08H118 09H018 09H079 10H014 10H038 11H002 11H014 11H046 11H138 11H170 12H030 12H149 13H039 13H048 13H056 13H083 14H012 14H019 14H027 02H009 02H025 02H043 02H053 02H060 02H066 03H024 03H033 03H036 03H081 03H090 03H094 03H116 03H119 04H001 04H006 04H024 04H025 04H048 04H055 04H103 04H108 04H112 04H117 04H120 04H127 04H133 04H135 04H138 05H008 05H022 05H030 05H034 05H078 05H111 05H163 05H184 05H195 06H028 06H029 06H088 06H089 06H103 06H144 06H151 07H060 07H062 07H107 07H112 07H125 07H133 07H135 07H137 07H151 07H152 07H158 07H160 08H012 08H034 08H048 08H053 08H056 08H065 08H082 08H085 08H113 08H129 09H002 09H022 09H026 09H031 09H040 09H043 09H045 09H048 09H070 09H078 09H083 09H088 09H090 09H113 09H115 10H040 10H048 10H056 10H068 10H070 10H092 10H095 10H107 10H109 10H113 10H115 11H010 11H019 11H035 11H058 11H097 11H103 11H107 11H129 11H135 11H142 11H151 11H186 11H232 11H240 12H010 12H021 12H039 12H056 12H079 12H091 12H116 12H171 12H172 12H173 12H175 12H176 13H073 13H080 13H139 13H150 13H158 13H169 14H001 14H017 14H020
plot (x[,c(1,2)], pch=20)
points (x[(rownames (x) %in% p.M6), c(1,2)], pch=20, col="yellow")
points (x[(rownames (x) %in% p.M5), c(1,2)], pch=20, col="orange")
points (x[(rownames (x) %in% p.M01), c(1,2)], pch=20, col="blue")
Figure 1: Deux composantes principales de la PCA appliquées à 285 échantillons de patients de Leucégène. Les couleurs correspondent à la classe FAB; les M0 et M1 sont représentés en bleu, les M5 en orange et les M6 en jaune.
Laisser un commentaire