Cette série d’articles sur l’apprentissage machine ne serait complète sans y couvrir le surapprentissage et la régularisation.
Le surapprentissage
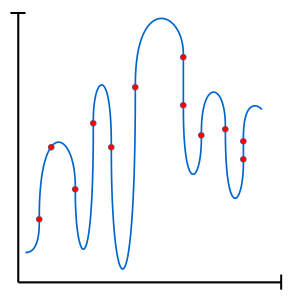
L’une des difficultés rencontrée lors de l’application de techniques d’apprentissage machine est le surapprentissage. Plus les techniques utilisées sont puissantes (grand nombre de paramètres libres), plus nous sommes susceptibles au surapprentissage.
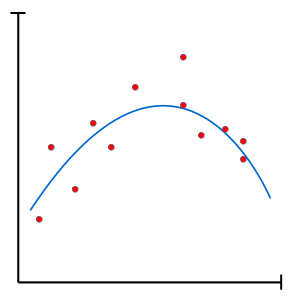
Lors du surapprentissage, le modèle diverge du principe du rasoir d’Occam en augmentant si bien son niveau de complexité qu’il finit par essentiellement mémoriser chaque détails de l’ensemble d’entraînement. Un modèle surentrainé peut donc difficilement généraliser sur de nouveaux cas.
Heureusement, le surapprentissage peut être contrôlé à l’aide de différentes techniques de régularisation afin de générer des modèles plus parsimonieux.
La régularisation
À la base, la régularisation tente de limiter le surapprentissage. Bien que certaines méthodes de régularisation peuvent s’avérer très complexes, certaines de ces méthodes sont surprenamment simples et directes. Par exemple, un modèle peut être forcé à généraliser simplement en limitant sa capacité (nombre de paramètres libres).
L’arrêt délibéré
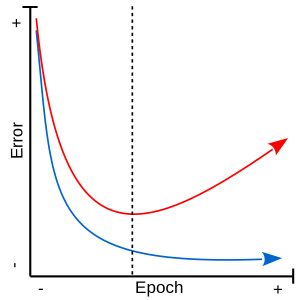
La méthode de l’arrêt délibéré (early stopping), souvent utilisée dans le cadre d’un entraînement par descente de gradient, a comme but d’arrêter l’entraînement lorsque le réseau donne des signes de surapprentissage. Lors d’un entraînement avec arrêt délibéré, une partie de l’ensemble d’entraînement est mise de côté et utilisée lors de l’entraînement comme ensemble de validation. Cette ensemble de validation, caché du modèle, offre un aperçu de la capacité de généralisation du modèle au cours de l’entraînement. L’entraînement est arrêté lorsque l’erreur de l’ensemble de validation commence à augmenter.
L1 / L2
La régularisation peut aussi s’introduire dans la fonction de coût. Les normes L1 ou L2 sont des termes ajouté à la fonction de coût en tant que terme de régularisation. L’ajout de tels termes de régularisation à la fonction de coût est un concept très populaire en apprentissage machine.
La régularisation par norme L1 (Lasso) tente de minimiser la somme des différences absolues entre valeurs réelles et valeurs prédites ($\theta_i$). Linéaire, elle offre la possibilité au modèle de facilement fixer un poids à 0 et peut donc, entre autres, faciliter la sélection de caractéristiques en forçant une représentation éparse (sparse).
$ L1 :\lambda\sum_{i=1}^n |\theta_i| $
La régularisation par norme L2 (Ridge / Tikhonov) tente de minimiser la somme des carrées des différences entre valeurs réelles et valeurs prédites ($\theta_i$). Ce terme est, entre autres, plus rapide à calculer que le terme L1. Exponentielle, elle promouvoit plutôt une représentation diffuse et, de ce fait, performe généralement mieux que la L1.
$ L2 : \lambda\sum_{i=1}^n \theta_i^2 $
Enfin, l’ampleur de l’effet du terme de régularisation est contrôlé grâce à un poids ($\lambda$) placé à l’avant du terme.
Voilà! J’espère vous avoir inspiré avec ce petit détour sur la problématique du surapprentissage et de quelques-unes des solutions offertes par régularisation. Comme toujours, restez à l’affût pour les prochaines mises à jours dans cette série d’articles sur l’apprentissage machine!


Quelles sont les différentes techniques de régularisations en apprentissage automatique ?