L’algorithme de descente de gradient est un algorithme itératif ayant comme but de trouver les valeurs optimales des paramètres d’une fonction donnée. Il tente d’ajuster ces paramètres afin de minimiser la sortie d’une fonction de coût face à un certain jeux de données. Cet algorithme est souvent utilisé en apprentissage machine dans le cadre de régressions non linéaires puisqu’il permet de rapidement trouver une solution approximative à des problèmes très complexes.
Mon dernier article, Introduction à la régression linéaire, fait mention de l’algorithme de la descente de gradient comme solution possible pour une régression linéaire simple. Bien qu’il existe une solution analytique optimale à la régression linéaire simple, la simplicité de ce problème en fait un excellent candidat pour démontrer l’application de l’algorithme du gradient.
Fonction de coût
Reprenons la fonction de coût pour une droite détaillée dans l’article Introduction à la régression linéaire. La sortie de cette fonction représente l’erreur et c’est cette erreur que l’on tentera de minimiser : la moyenne de la distance verticale entre nos observations et la droite de régression au carrée (voir la méthode des moindres carrées). Afin de garder une erreur de taille raisonnable et qui ne sera pas affectée par la taille de notre jeu de données, nous divisions par le nombre d’observations pour récupérer la moyenne des erreurs.
$ Coût = \dfrac{\sum_{i=1}^n(y_i-(m x_i + b))^2}{N} $
Gradient
Le gradient (la pente de notre fonction de coût à un point donné) représente la direction et le taux de variation de notre fonction de coût. Suivre le gradient négatif de la fonction nous permet donc de la minimiser le plus rapidement possible. Afin d’obtenir le gradient, notre fonction doit être différentiable. Prendre le carré de la distance nous assure une erreur positive et ainsi une fonction différentiable.
Le gradient de notre fonction de coût est obtenu en prenant la dérivée en fonction de nos paramètres $m$ et $b$ :
$ \dfrac{\delta}{\delta m} = \dfrac{2\sum_{i=1}^n-x_i(y_i-(m x_i + b))}{N} $
$ \dfrac{\delta}{\delta b} = \dfrac{2\sum_{i=1}^n-(y_i-(m x_i + b))}{N} $
Deux paramètres doivent êtres fixés dans l’algorithme du gradient, soit le pas de gradient (le taux de changement à chaque itération) et le nombre d’itérations ou époques pour l’apprentissage. Dans notre exemple, l’algorithme tentera d’ajuster les paramètres $m$ et $b$ durant 10 000 itérations (epochs) avec un pas de gradient (lr) de 0.001.
Code
import matplotlib.pyplot as plt
import numpy as np
# Fonction de coût
def error(m, b, X, Y):
return sum(((m * x + b) - Y[idx])**2 for idx, x in enumerate(X)) / float(len(X))
# Gradient du paramètre m
def m_grad(m, b, X, Y):
return sum(-2 * x * (Y[idx] - (m * x + b)) for idx, x in enumerate(X)) / float(len(X))
# Gradient du paramètre b
def b_grad(m, b, X, Y):
return sum(-2 * (Y[idx] - (m * x + b)) for idx, x in enumerate(X)) / float(len(X))
def gradient_descent_LR(X, Y, epochs, lr):
assert(len(X) == len(Y))
m = 0
b = 0
for e in range(epochs):
m = m - lr * m_grad(m, b, X, Y)
b = b - lr * b_grad(m, b, X, Y)
return m, b
if __name__ == '__main__':
# Génération du jeu de données
X = np.linspace(-1, 1, 100) + np.random.normal(0, 0.25, 100)
Y = np.linspace(-1, 1, 100) + np.random.normal(0, 0.25, 100)
# Exécution de l'algorithme
m, b = gradient_descent_LR(X, Y, epochs=10000, lr=0.001)
# Visualisation de la droite avec les valeurs de m et b trouvées par descente de gradient
line_x = [min(X), max(X)]
line_y = [(m * i) + b for i in line_x]
plt.plot(line_x, line_y, 'b')
plt.plot(X, Y, 'ro')
plt.show()Visualisation de l’entraînement
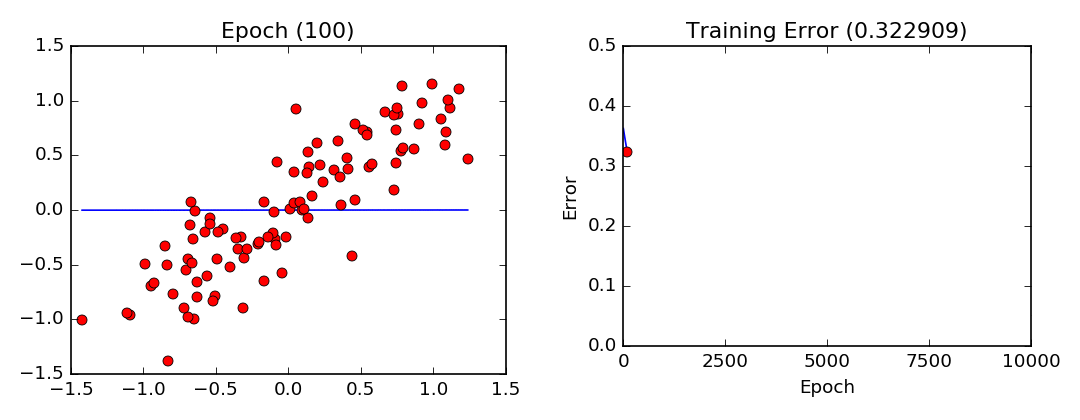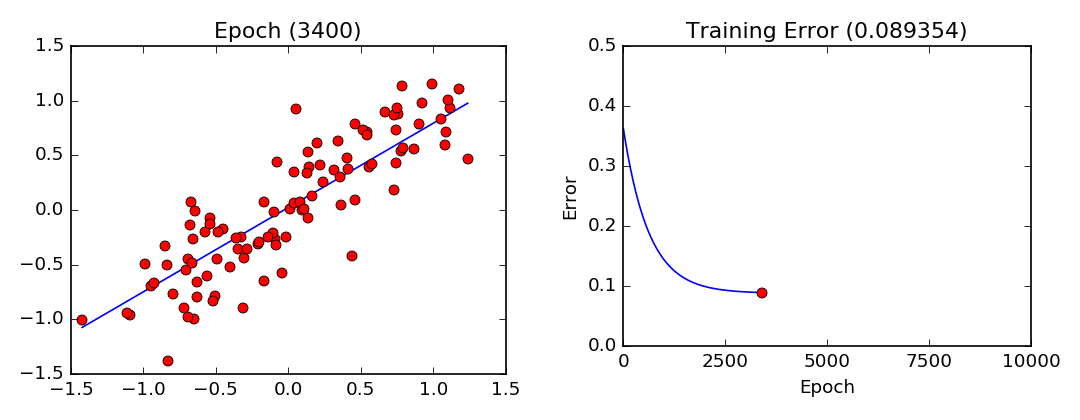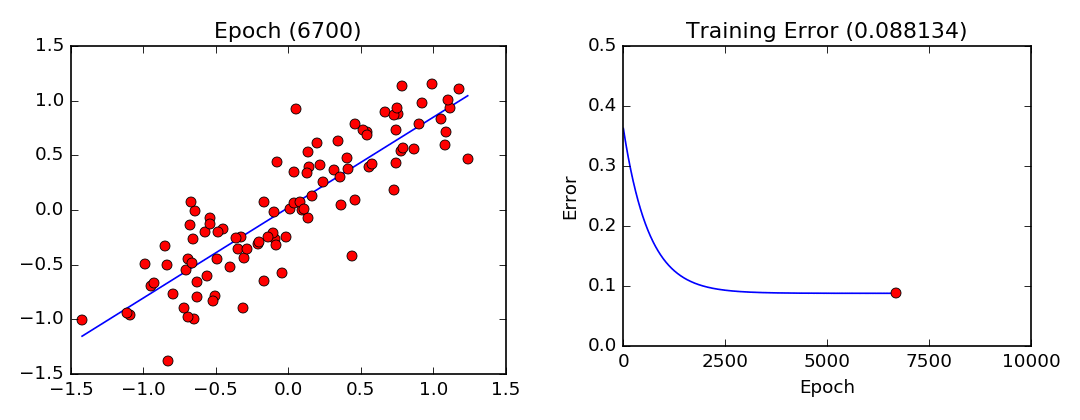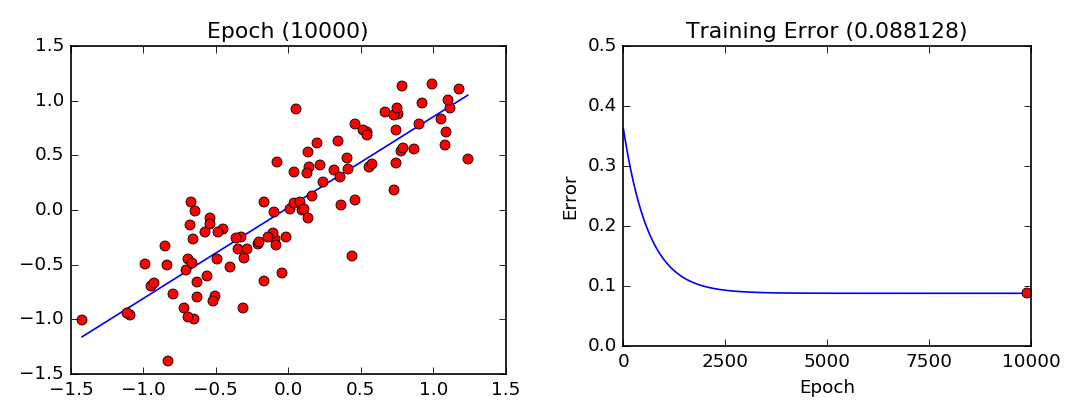
Visualisation de l’entraînement par descente de gradient. Notez que les paramètres convergent de plus en plus lentement lorsqu’ils approchent de leurs valeurs optimales.
Un excellent article couvrant le même sujet plus en détails peut être retrouvé à l’addresse suivante (en anglais) : https://spin.atomicobject.com/2014/06/24/gradient-descent-linear-regression/.


Laisser un commentaire