Lorsqu’on travaille avec toutes sortes de données, il arrive parfois que nous voulons prédire la valeur d’une variable qui n’est pas numérique. Dans ces cas-là, la régression logistique est tout à fait appropriée. On peut dire qu’elle est s’apparente à une régression linéaire sauf que la variable dépendante est une catégorie.

Vous vous souvenez de la fonction de la régression linéaire où l’on essaie d’estimer les paramètres beta (les coefficients) qui s’ajustent le mieux la droite à nos données:

\begin{equation}
Y_i = \beta_0 + \beta_1 X_i + \epsilon_i
\end{equation}

Et bien, dans une régression logistique, nous essayons aussi d’estimer les paramètres beta mais pour :
\begin{equation}
y = \left\{\begin{matrix}1\: \: \: \: Y_i = \beta_0 + \beta_1 X_i + \epsilon_i > 0
\\
0\: \: \: \:else
\end{matrix}\right.
\end{equation}

Ici, y n’est pas linéairement dépendant de x. Regardons maintenant un exemple!

Prédire le sexe à partir des profils d’expression des gènes

Lorsque je construis un modèle à partir de l’expression des gènes, je commence habituellement par essayer de construire un modèle pour prédire le sexe. Ça me sert de contrôle puisque c’est une tâche très facile à effectuer. On peut facilement prédire le sexe en regardant l’expression de seulement quelques gènes.

Pour mon example, j’ai décidé d’utiliser le jeu de données de RPKM du Genotype-Tissue Expression (GTEx) . Le portail de GTEx permet d’explorer les données transcriptomiques et les associations génétiques à travers différents types de tissus cellulaires provenant de donneurs décédés en bonne santé. La version V6p contient 8555 échantillons sondant 53 tissus provenant de 544 donneurs post-mortem. Vous devriez  jeter un coup d’oeil au site, c’est vraiment intéressant et leurs outils sont faciles à utiliser.


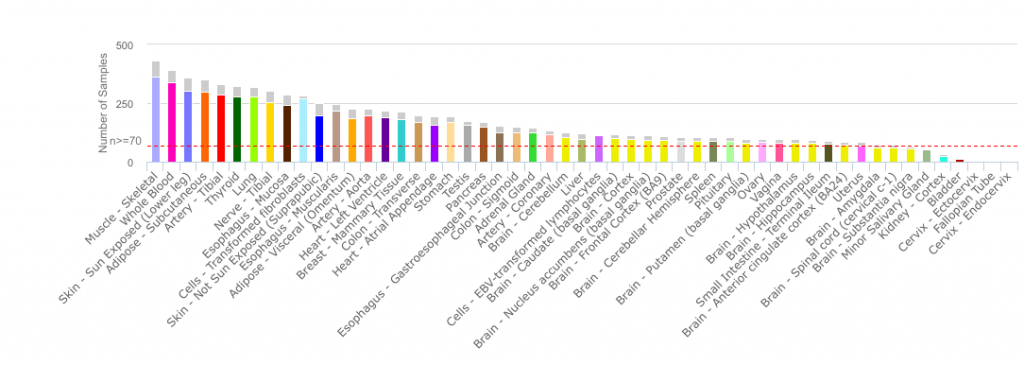Figure1.Distribution of the tissues samples in the GTEx cohort [source:http://www.gtexportal.org/home/tissueSummaryPage]
 

Comme le jeu de données de GTEx est assez gros (56238 rangées par 8555 colonnes), j’ai utilisé python pour faire ma régression logistique en utilisant les fonctions de scikit-learn package. Si vous avez un jeu de données plus petit, la fonction R glm(formula, data=mydata, family='binomial') (avec ces paramètres) est ce que vous cherchez.

Donc, c’est parti. Avant de commencer, j’ai : 1) lire la matrice de RPKM, les annotations des échantillons et les annotions sur les donneurs, 2) log-transformer les valeurs de RPKM (log10(RPKM+0.01)) 3) filtrer les gènes pour ne garder que les 10 000 gènes les plus variables. J’ai gardé un peu moins de 20% des gènes pour mon exemple, c’était un choix tout à fait arbitraire.

 

SMCENTER SMTS SMTSD SUBJECT
GTEX-1117F-0003-SM-58Q7G B1 Blood Whole Blood GTEX-1117F
GTEX-1117F-0003-SM-5DWSB B1 Blood Whole Blood GTEX-1117F
GTEX-1117F-0226-SM-5GZZ7 B1 Adipose Tissue Adipose – Subcutaneous GTEX-1117F
GTEX-1117F-0426-SM-5EGHI B1 Muscle Muscle – Skeletal GTEX-1117F
GTEX-1117F-0526-SM-5EGHJ B1 Blood Vessel Artery – Tibial GTEX-1117F

Table1. Exemple de données de GTex.


Lorsqu’on essaie de prédire quelque chose, il est toujours recommandé de travailler avec un ensemble d’entrainement et un ensemble de test. Vous construisez votre modèle en utilisant l’ensemble de données d’entrainement et vous évaluez sa performance en utilisant l’ensemble de test. La plupart des fonctions de scikit-learn sont faites pour fonctionner dans ce cadre.


from sklearn.linear_model import LogisticRegression
from sklearn import metrics, cross_validation
from sklearn.cross_validation import train_test_split
from sklearn.cross_validation import cross_val_score

# X est la matrice de gènes, 
# Y est le vecteur contenant le sexe de chaque donneur
# 0.3 indique que 30% des données constitueront l'ensemble de test et 70%, 
# l'ensemble d'entrainement

X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=0)

# Ces paramètres servent à restreindre les variables considérées par le modèle
model = LogisticRegression(penalty='l2', C=0.2)  
model.fit(X_train, y_train)

# On applique le modèle à l'ensemble de test
predicted = model.predict(X_test)
probs = model.predict_proba(X_test)

Voilà! Je peux maintenant regarder les prédictions pour évaluer la performance du modèle. Comme il y avait 62.3% d’hommes dans mon ensemble de test (ce qui est proche de la proportion d’homme dans le jeu de données complet), le modèle a besoin de faire une bonne prédiction plus de 62.3% du temps pour que l’on puisse dire qu’il est performant. Sinon, il pourrait seulement décider de toujours prédire ‘Male’ (sans se fier aux données d’expression) et il serait correct 62.3% du temps. Dans cet exemple, le modèle a une précision (accuracy) de 100%. Il fait la bonne prédiction pour tous les échantillons.

Ensuite, en regardant les coefficients beta, je peux identifier les gènes qui servent dans le modèle pour prédire le sexe. Ce sont les gènes avec les plus grands et plus petits coefficients. Dans ce cas-ci, le top 4 gènes incluent :
RPS4Y1 (coefficient de 1.34), KDM5D (1.27), DDX3Y (1.25) and XIST (-1.25). Notez que XIST est le seul gène qui semble spécifique aux femmes.


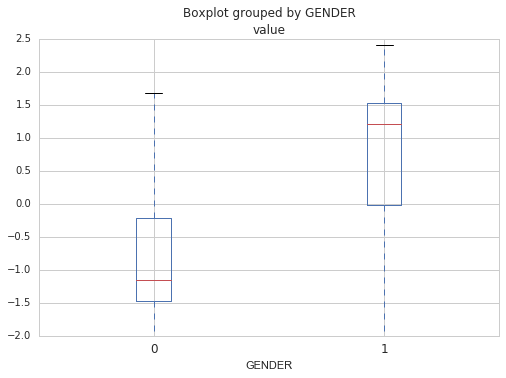Figure2. Distribution de l’expression log-transformée des 10 gènes avec les coefficients les plus importants.
 

Notez que vous devriez toujours faire une validation croisée pour être certain que le modèle n’est pas spécifique à votre jeu de données (qu’il ne sur-apprend pas). Le but, après tout, quand on construit des modèles prédictifs est de pouvoir les réutiliser sur de nouvelles données, donc il doit être capable de généraliser. La validation croisée implique rouler le générer un même modèle plusieurs fois en utilisant différents ensemble d’entrainement et de test et regarder le score moyen pour avoir une idée de la performance réelle du modèle. Dans le code ci-dessous, le modèle set construit 10 fois en utilisant chaque fois un différent ensemble de test et un différent ensemble d’entrainement. Le score moyen des 10 itérations est rapporté et nous indique si la généralisation est bonne.


# Évaluer le modèle par une validation croisée
scores = cross_val_score(LogisticRegression(penalty='l2', C=0.2), xx.T, Y, scoring='accuracy', cv=10)

Prédire le tissu à partir des données d’expression de gènes

Maintenant pour le plaisir, je peux tenter de dériver un modèle qui prédira le tissu de provenance de l’échantillon. Je dis pour le plaisir parce que je ne ferai pas de validation croisée, je regarderai un seul modèle, et parce qu’il y a un nombre différent de d’échantillons dans chaque catégorie de tissu. Une catégorie contient 1259 échantillons alors qu’une autre en contient 6. J’aurais sans doute besoin d’évaluer comment cela affecte le modèle et de faire des changements en conséquence.

Mais juste pour le plaisir, il y a 31 tissus de plus haut niveau dans le jeu de données, les deux plus représentés étant « Brain » et « Skin », respectivement 14.7% et 10.4% des échantillons. En utilisant le même code et la même matrice de gènes qu’auparavant, en changeant seulement le vecteur Y qui contient les valeurs de la variable dépendant à prédire, j’obtiens un bon modèle qui a raison dans 99.3 % du temps. Il a fait 18 erreurs sur un total de 2567 prédictions. C’est intéressant de voir que parmi ces erreurs, un bon nombre implique des tissus féminins. C’est peut-être dû au fait que les échantillons féminins sont sous-représentés dans le jeu de données.

Prédite Réelle
Stomach Vagina
Nerve Adipose Tissue
Esophagus Stomach
Colon Small Intestine
Esophagus Stomach
Esophagus Stomach
Colon Esophagus
Skin Vagina
Uterus Fallopian Tube
Adipose Tissue Breast
Ovary Fallopian Tube
Skin nan
Blood Vessel Uterus
Adipose Tissue Stomach
Stomach Colon
Esophagus Stomach
Heart Blood Vessel
Adipose Tissue Fallopian Tube

Table2. Erreurs de prédiction faites par le modèle.