Contexte:
AUC est un acronyme pour « Area Under the (ROC) Curve ». Si vous n’êtes pas familier avec les notions de courbe ROC et d’AUC, je vous suggère de commencer par ce blog post avant de continuer.
Dans plusieurs projets, il m’a fallu calculer un grand nombre d’AUC. J’ai commencé par devoir en calculer 25000, puis 230000 et, maintenant, j’en suis au tour de 1,5 million. Avec autant d’AUC, le temps nécessaire pour calculer une AUC devient un paramètre critique. Je n’ai pas trouvé beaucoup d’information sur ce sujet spécifique, il est probable que cette contrainte ne soit pas souvent rencontrée dans la communauté.
Ainsi, l’objectif de cet article est de faire une revue complète des méthodes existantes en fonction de leurs temps d’exécution. Si jamais vous connaissez une autre méthode n’hésitez pas à laisser un commentaire, merci.
Analyse:
Partant d’un vecteur de scores (avec des étiquettes):
| Label: | A | A | A | A | … | B | B | B | B |
| Score: | 10 | 20 | 15 | 5 | … | 8 | 12 | 9 | 3 |
J’ai trouvé 3 méthodes pour calculer une AUC:
- Aire des trapézoïdes: il faut commencer par transformer le vecteur de scores en un vecteur de coordonnées (qui représente la courbe ROC) et calculer l’aire de chaque trapézoïdes.
- Mesure de concordance: il faut comparer toutes les paires possibles et de compter le nombre de fois où le Score(A) > Score(B).
- À partir du test Mann Whitney: on utilise le calcul de la statistique U.
Maintenant, je vous propose d’identifier la méthode la plus rapide en estimant le nombre d’opérations nécessaires pour chaque stratégie. Globalement, si on a besoin de plus d’opérations, alors le calcul devrait être plus long. Estimer le nombre d’opérations est un sujet vaste appelé la complexité, mais ici je propose une approche simplifié:
- La mesure de concordance nécessite n*m comparaisons, avec n (resp. m) le nombre d’échantillons A (resp. B). Cette méthode fait partie des algorithmes dit quadratiques, le nombre d’opérations augmente de façon exponentielle avec le nombre d’échantillons. Il est possible de réduire le nombre d’opérations en comparant seulement un sous-ensemble de paires (n*m*p, with 0<p<1). Chaque paire doit être choisie aléatoirement avec remise. Attention cette astuce ne fait qu’échanger de la précision (au niveau du calcul de l’AUC) contre du temps, et trouver la « taille optimale » du sous-ensemble n’est pas forcément évident.
- u-test: Pour calculer la statistique U, nous avons principalement besoin de calculer le rang de chaque échantillon en fonction de son score, ce qui peut être fait avec un algorithme de tri en N*log(N) opérations (avec N=n+m).
- Calcul de l’aire commence par trier le vecteur pour transformer les scores en coordonnées. Il est ensuite possible de calculer et de faire la somme de l’aire des N-1 trapézoïdes. Ceci nécessite N*log(N) + N opérations.
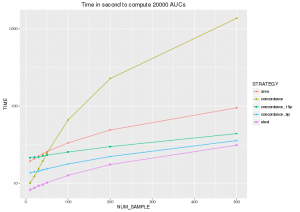
Ainsi, c’est le U-test qui calcule l’AUC avec le moins d’opérations et qui devrait être la méthode la plus rapide. Pour vérifier ce résultat de façon concrète, j’ai implémenté toutes ces méthodes en python3 et j’ai obtenu la figure ci-dessous.
« concordance_15p » (resp. « concordance_5p ») représente la méthode « concordance » appliquée à un sous-ensemble de paires avec p=0.15 (resp. 0.05).
Comme on peut le voir:
- Mann Whitney/u-test est bien la méthode la plus rapide, si on n’a pas besoin des coordonnées pour afficher la courbe ROC.
- Le temps de calcul de l’aire progresse de manière similaire à celui du u-test (les 2 méthodes sont dans la catégories des algorithmes pseudo linéaires). Comme on pouvait s’y attendre, il est toutefois 2 fois plus lent que le u-test: N*log(N) + N = 2* N*(log(N)+1).
- Comme pour le nombre d’opérations, le temps de calcul de la concordance augmente de façon exponentielle avec le nombre d’échantillons.
- Le calcul de la concordance sur un sous-ensemble est toujours plus lent que le calcul du u-test. Je n’ai pas mesuré la précision des estimations de l’AUC, mais je ne vois aucun avantage à utiliser cette méthode. En fait, je ne comprends pas pourquoi cette méthode est si souvent citée contrairement au u-test.
Ci-dessous vous trouverez l’implémentation du « u-test » en R et python. Les implémentations de toutes ces méthodes sont d’ailleurs disponibles sur mon git.
| R | Python |
|
|
sources: stackexchange, wikipedia, stackoverflow


Laisser un commentaire