Les boxplots ou diagramme de quartiles sont partout! Les éditeurs aiment les diagrammes de quartiles. Mais demandez à quelques personnes et la plupart ne pourront même pas vous expliquer ce que représente cet amas de lignes!
Récemment, j’ai voulu examiner l’expression génique entre deux échantillons pour un certain gène. Le graphique standard pour ceci est bien sûr ***roulement de tambour***… Le boxplot!
Fait intéressant #1: Saviez-vous que les diagrammes de quartiles sont également appelés « boîte moustache »*?
Et si on les regardait de plus près? Un boxplot est généré aisément avec un logiciel d’analyse, tel que R, et son interprétation est intuitive, mais il y reste quelques nuances.
Décortiquons-le ensemble!
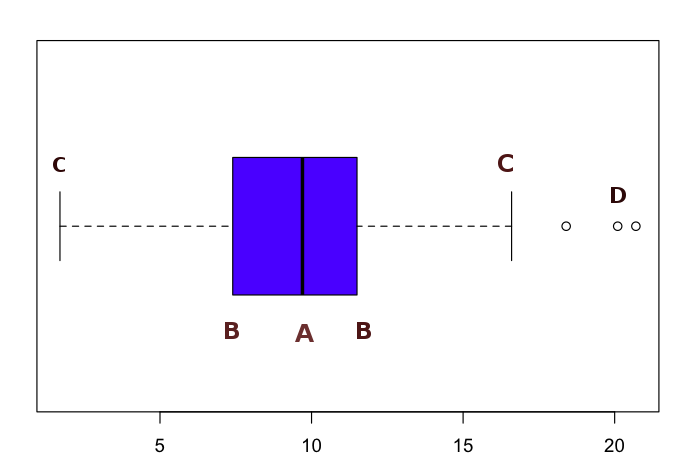
A- Cette ligne est une médiane
Qu’est-ce que la médiane? Si vous ne le savez pas, continuez votre lecture, on vous explique! Si vous mettiez toutes les valeurs en ordre croissant, la médiane serait la valeur du milieu. Par exemple, pour les valeurs 1,5,6,12,17,18,21 : la médiane est 12. C’est la valeur au centre. Attention de ne pas la confondre avec la moyenne. Dans ce cas-ci, la moyenne est 11.42.
Mais alors, que fait-on si on a un nombre de valeurs pair? Par exemple, 1,3,4,5,19,156. La médiane ici est la moyenne des deux valeurs du milieu, alors $(4+5)/2 = 4.5$. Encore une fois, ne pas confondre avec la moyenne, qui est ici de 31.33.
B- Ces deux lignes représentent la séparation des 1er et 3ème quartiles
Un quartile est un peu comme une médiane, mais divisée en quatre au lieu de 2. Ici, les lignes B représentent respectivement les premier (Q1 ou quartile inférieur) et troisième (Q3 ou quartile supérieur) quarts des valeurs.
C- Les moustaches
Dans un boxplot Tukey, ces lignes représentent 1.5*IQR (l’écart interquartile ou interquartile range). Cette curieuse valeur est la distance (lire différence) entre les valeurs Q3 et Q1, qui sont les 3ème et 1er quartiles. Dans certains boxplots, les moustaches représentent les valeurs minimum et maximum.
D- Données aberrantes (Outliers)
Et il y a eux, les aberrants. Ce sont des données qui ne sont pas incluses ni dans les lignes 1.5*IQR (moustaches), ni dans la boîte principale. Ces données nous donnent des indices sur la distribution, chose qu’il est impossible de visualiser avec la boîte. Notez que les données aberrantes ne sont pas toujours représentées.
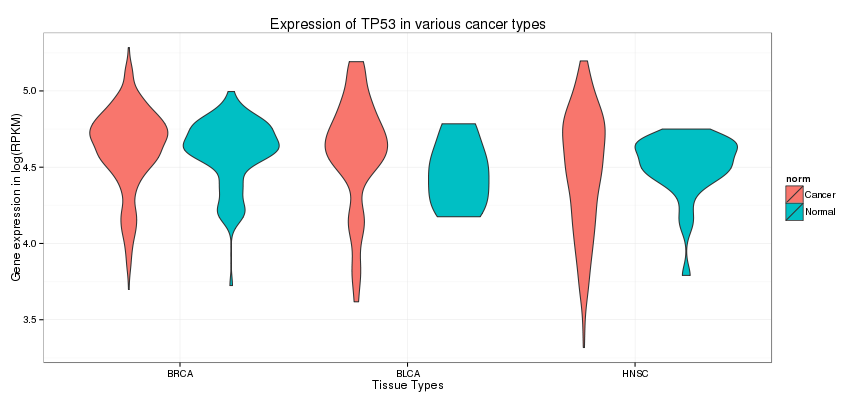
Dans d’autres cas, les violin plots sont utilisés. Ces graphiques montrent la distribution d’une plage de données. Plus il y a d’entrées ayant la même valeur, plus le graphique sera large à cette valeur. Ci-dessous est un graphique violon avec l’expression du gène TP53 dans les échantillons cancer versus normal, pour les cancers suivants: de la vessie (BLCA), du sein (BRCA) et de la tête et du cou (« Head and Neck », abrévié HNSC)
Poussons un peu plus loin!
La valeur IQR est utile pour vérifier la normalité d’une plage de données (distribution Gaussienne). Disons que vous détenez un ensemble de données dont vous connaissez l’écart-type, la moyenne ainsi que les valeurs Q1 et Q3. Si la distribution est normale, la valeur Q1 devrait correspondre à la somme de la moyenne ($\underline{x}$) plus -0.67 fois l’écart-type ($\sigma$). Comme ceci: $Q1 = \overline{x}+(-0.67*\sigma)$. Et la même chose s’applique pour Q3, sauf que c’est 0.67 fois l’écart-type: $Q3 = \overline{x}+(0.67*\sigma)$.
Les boxplots sont un bon moyen pour apprendre à connaître ses données. Laissez-les vous raconter leur histoire, vous n’avez qu’à écouter…à condition de poser les bonnes questions, bien sûr!
** Les diagrammes de quartiles sont aussi appelés tracé en boîtes, tracés en rectangles et moustaches ou tout simplement, boîtes à moustaches.


Merci beaucoup pour ces précieuses informations