Comprendre la réduction de dimensionalité
Si vous utilisez de larges jeux de données (transcriptomes, séquençage de génome, protéomes), tôt ou tard, vous tomberez sur quelque chose qui porte le nom « d’analyse de composantes principales » (Principal Components Analysis, en anglais, abrévié PCA). PCA est une méthode de réduction de dimensionalité, une famille large de méthodes qui font exactement ce que leur nom dit: elles réduisent la dimensionalité.
Mais qu’est-ce que ça veut dire? Qu’est-ce qu’une dimension et pourquoi on voudrait les réduire?
Voici un exemple répondant à ces questions
La problématique
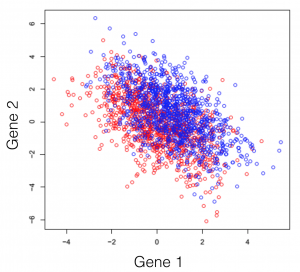
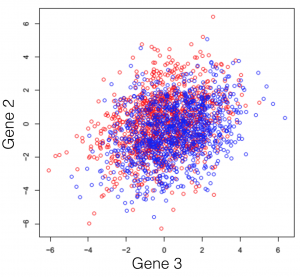
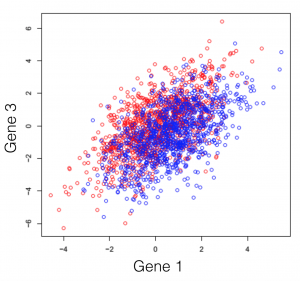
Disons que vous faites face à un transcriptome hypothétique, d’une espèce primitive qui a un total de 3 gènes dans son génome. Certains des individus de cette espèce ont été traités avec un composé chimique et vous observez le changement d’expression des 3 gènes de l’organisme. Si vous tracez les trois combinaisons de gènes, vous obtenez les trois graphiques suivants (les couleurs symbolisent les deux conditions expérimentales). Note générale: l’emploi du mot dimensions n’est ici qu’un terme spécial pour désigner les gènes.
On peut observer une tendance dans l’expression des gènes séparant les deux conditions (les rouges des bleus), cependant, elle demeure impossible à extraire. Cette tendance, à peine visible à l’oeil, peut être distillée utilisant des techniques de réduction de dimensionalité. Réduire les dimensions ne veut pas dire en jeter certaines et en garder d’autres. Cette famille de méthodes tente plutôt de se débarrasser de redondances, en créant un nouveau système de dimensions, qui expliquerait mieux les observations dans le jeu de données. Dans l’article suivant (et les prochains) je tenterai de fournir une explication intuitive de ce que chaque type de réduction de dimensionalité fait.
Analyse de composantes principales
La PCA, spécifiquement, tente de créer un nouveau système de coordonnées qui explique le mieux la variabilité dans les échantillons. En d’autres mots, la PCA cherche une direction dans les données, qui sépare le mieux les échantillons. Une fois la direction trouvée, elle cherche la deuxième, « meilleure séparatrice », etc.
Il y a cependant un détail technique: chaque nouvelle direction (ou dimension) trouvée doit être orthogonale aux autres. Orthogonal fait référence à un angle droit et la raison du choix d’orthogonalité des dimensions est, entre autres, due au fait que dans l’espace d’origine, les dimensions sont orthogonales l’une à l’autre.
Des fois, on réfère à la PCA comme une rotation. La rotation est en fait appliquée sur l’espace du jeu de données pour trouver les dimensions les plus séparantes. Dans la gif ci-dessous (cliquez pour voir l’animation), on peut voir une rotation qui sépare facilement les deux groupes d’individus selon les conditions expérimentales.
Si vous aviez à expliquer comment cette rotation est faite, intuitivement vous direz que la rotation n’est qu’un angle dans lequel on a tourné l’espace des gènes. Sachant qu’un angle est une combinaison linéaire de deux dimensions, la rotation peut donc être résumée à une combinaison linéaire des dimensions (ou gènes) d’entrée.
Une autre observation importante est que soudainement, vous n’avez plus besoin de représenter le jeu de données en 3 dimensions (1 dimension par gènes). Vous pouvez plutôt le tracer en deux dimensions où chaque nouvelle dimension du nouveau système de coordonnées est une combinaison des gènes.



Laisser un commentaire